Two capacitors having capacitances C1 and C2 are charged with 120 V and 200 V batteries respectively. When they are connected in parallel now, it is found that the potential on each one of them is zero. Then,
9C1=4C2
5C1=3C2
3C1=5C2
5C1=−3C2
The correct Answer is:C
C=QV ∴Q1=120C1,Q2=200C2
since the potential becomes zero, the net charge on the combination must be zero.
∴Q1+Q2=0 ∴120C1=−200C2 ∴3C1=−5C2.
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP20videos
ELECTROSTATICS
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 1715videos
ELECTRONS AND PHOTONS
- BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -220videos
GRAVITATION
Similar Questions
Two capacitors with capacities C1 and C2 ,are charged to potentials V1 and V2 respectively.When they are connected in parallel,the ratio of their respective charges is ....?
View SolutionTwo capacitors of capacitance 10 μF and 20 μF are charged to potential 20 V and 10 V respectively. If they are connected to share charges, then loss of energy is
View Solution
Knowledge Check
- Question 1 - Select One
Two capacitors having capacities C1andC2 are charged to voltages V1andV2 respectively. There will be no exchange of energy in connecting them in parallel, if
AC1=C2BC1V1=C2V2CV1=V2DC1V1C2V2 - Question 2 - Select One
Two capacitors with capacities C1 and C2 ,are charged to potentials V1 and V2 respectively.When they are connected in parallel,the ratio of their respective charges is ....?
AC1=C2BC1V1=C2V2CV1=V2DC1V1=C2V2 - Question 3 - Select One
Two capacitors C1 and C2 are charged to 120V and 200V respectively. It is found that connecting them together the potential on each one can be made zero. Then
A(a) 5C1=3C2B(b) 3C1=5C2C(c) 3C1+5C2=0D(d) 9C1=4C2
Two capacitors of capacitances 3μFand6μF, are charged to potentials 2V and 5V respectively. These two charged capacitors are connected in series. Find the potential across each of the two capacitors now.
View SolutionTwo capacitors of capacitances 3μF&6μF are charged to potential of 2V and 5V respectively.These two charged capacitors are connected in series.Find the potential across C1
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.
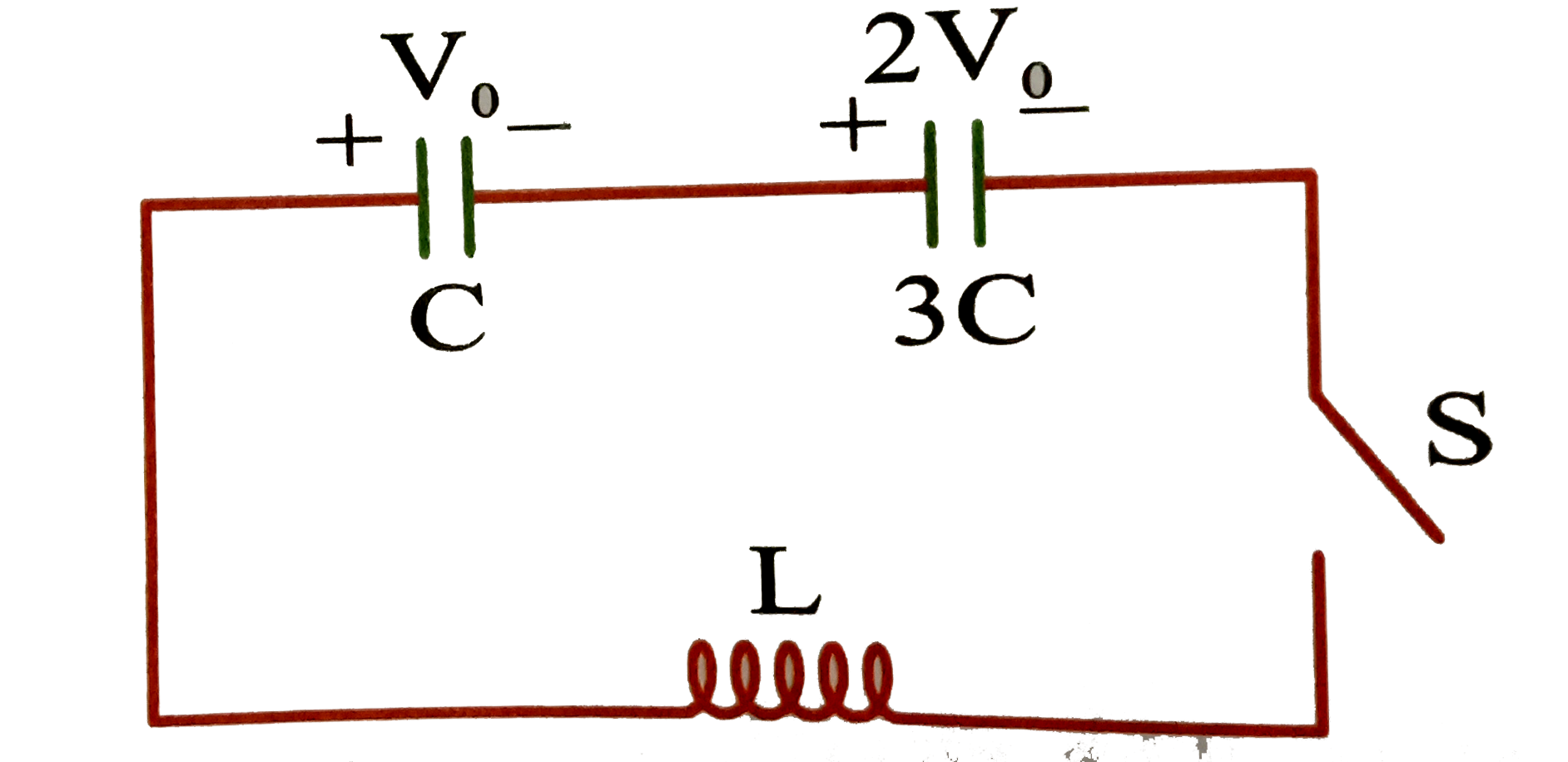
Potential difference across capacitor of capacitance C when the current in the cirucit is maximum isView SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.
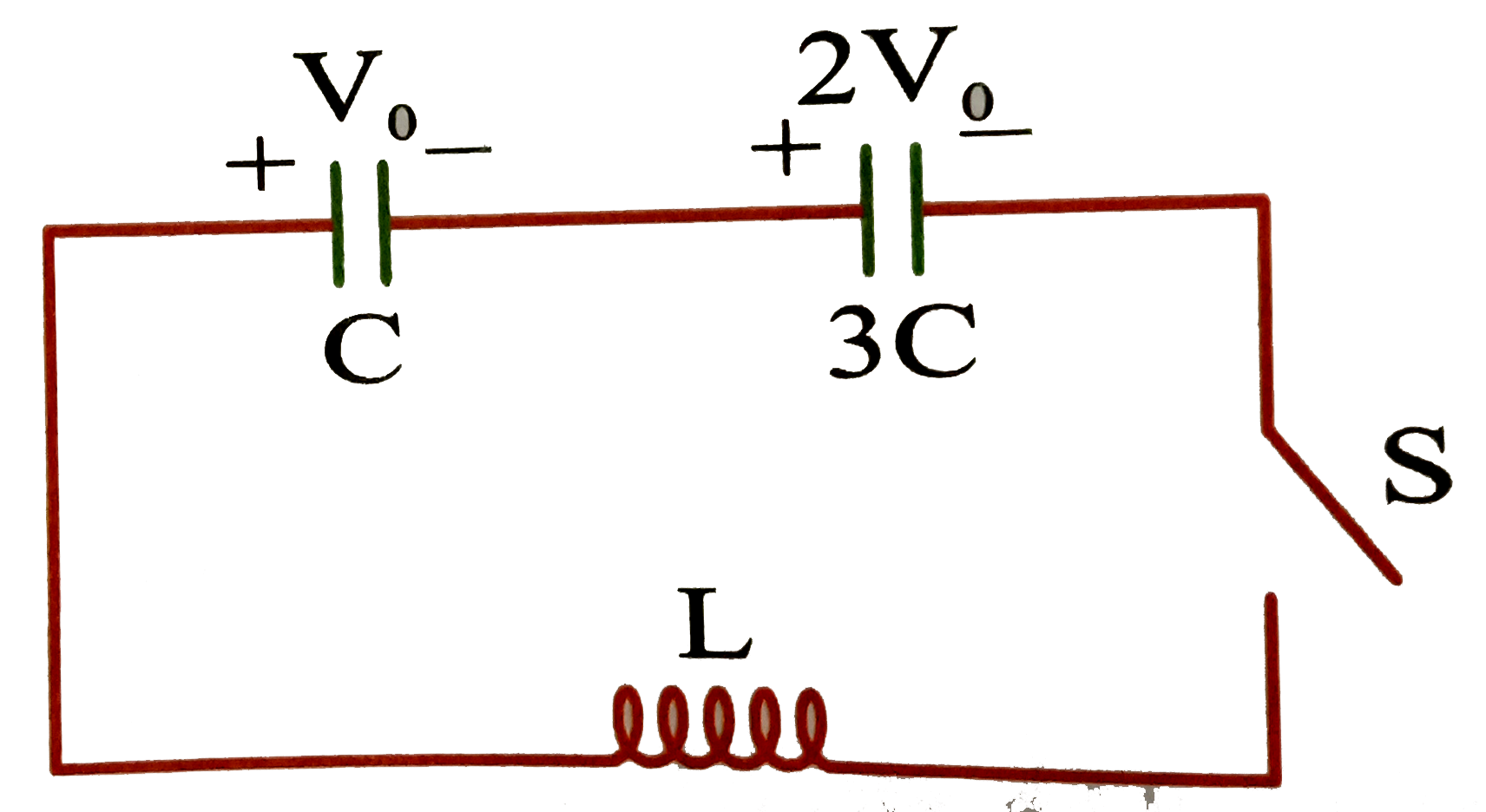
Potential difference across capacitor of capacitance 3C when the current in the cirucit is maximum is :View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
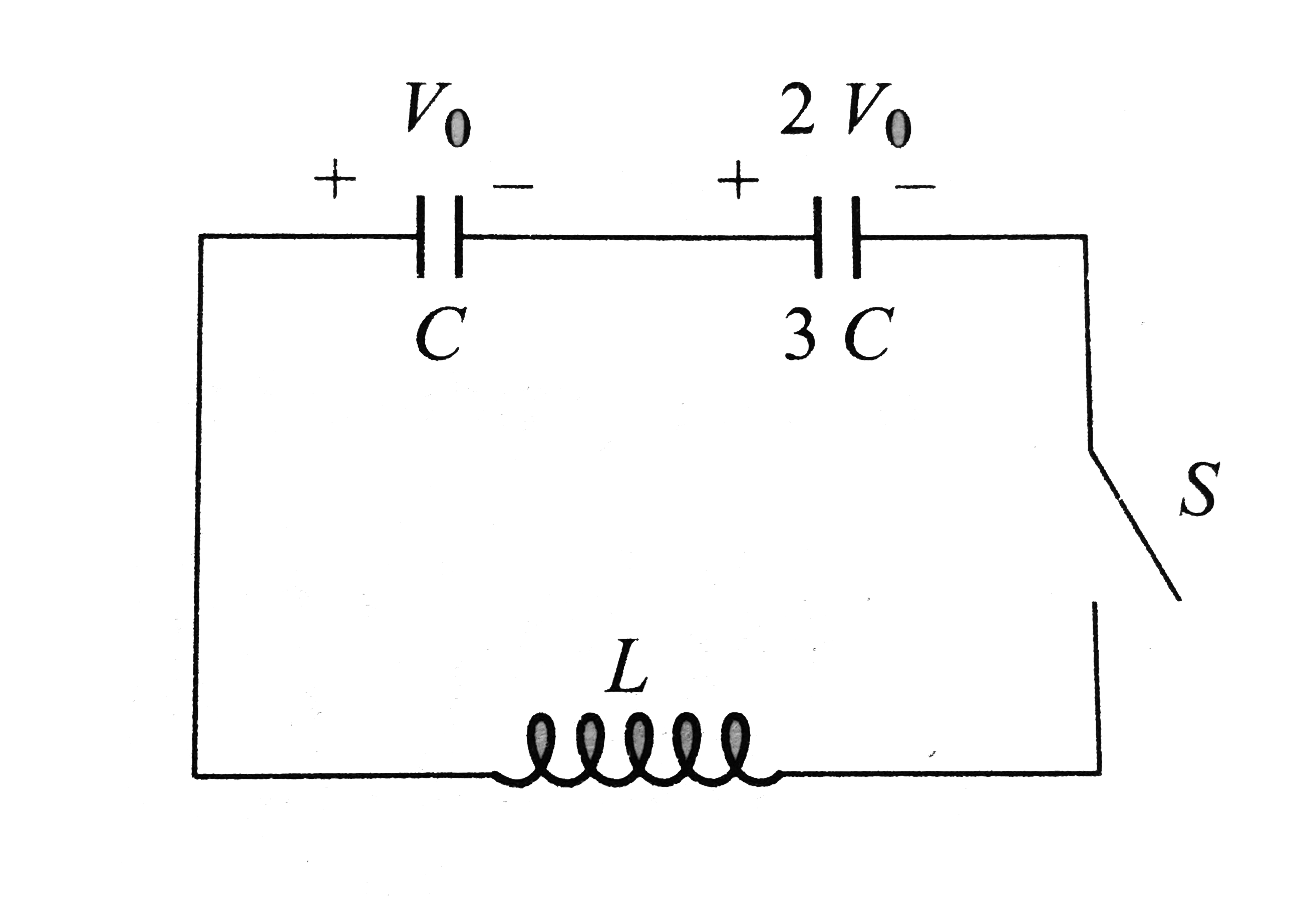
Potential difference across capacitor of capacitance C when the current in the circuit is maximum isView Solution

