Two cars start off a race with velocity 2ms−1 and 4ms−2 respectively. What is the length of the path if they reach the final point at the same time ?
Let both particles reach at same position in same time t then from s=ut+12at2
For 1st particle, s=4(t)+12(1)t2=4t+t22,
For 2nd particle, s=2(t)+12t2=2t+t2
Equations, we get 4t+t22=2t+t2⇒t=4s
Substituting value of t in above equations, we get
s=4(4)+12(1)(4)2=16+8=24m
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.1
10 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.2
10 Videos
- MOTIONBOOK - DC PANDEYCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
Two cars start off a race with velocities 2m/s and 4m/s travel in straight line with uniform acceleration 2m/s2and1m/s2 respectively. What is the length of the path if they reach the final point at the same time ?
View SolutionTwo car travelling towards each other on a straith road at velocity 10ms−1 and 12ms−1 respectively. When they are 150 m apart, both the drivers apply their brakes and each car decelerates at 2ms−2 until it stops. How far apart will they be when both of them come to a halt ?
View Solution
Knowledge Check
Two cars start in a race with velocities u1 and u2 and travel in a straight line with acceleration α and β. If both reach the finish line at the same time, the range of the race is
A2(u1−u2)(β−α)2(u1β−u2α)B2(u1−u2)β+α(u1α−u2β)C(2u1−u2)2(β−α)2D2u1u2βαTwo cars start off to race with velocities 4m/sand2m/s and travel in straight line with uniform accelerations 1m/s2 respectively. If they reach the final point at the same instant, then the length of the path is.
A30 mB32 mC20 mD24 mTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
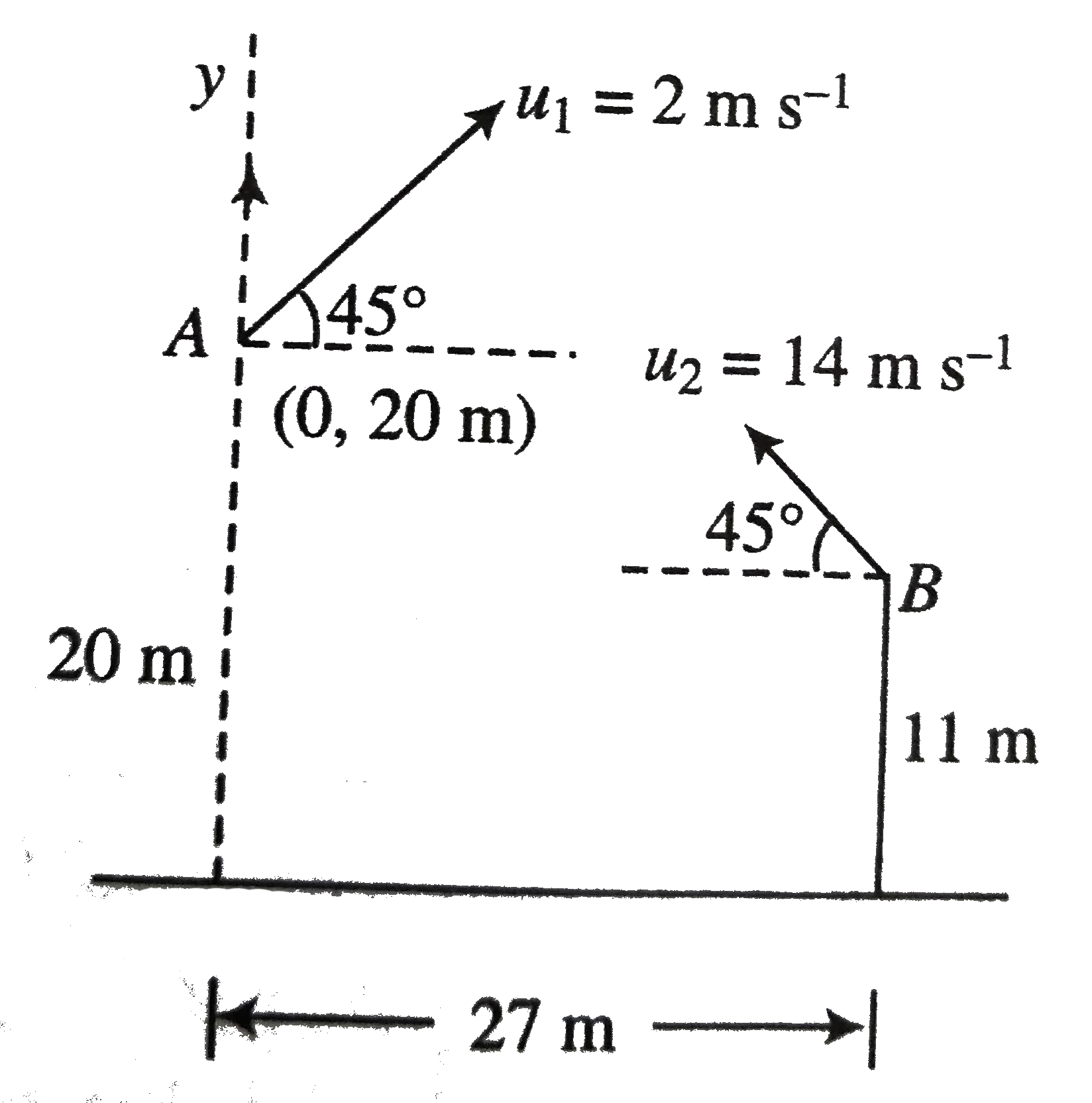
The relative velocity of B as seen from A inA−8√2ˆi+6(√2)ˆjB4√2ˆi+3(√3)ˆjC3√5ˆi+2(√3)ˆjD3√2ˆi+4(√3)ˆj
Three small balls of masses 1kg, 2kg and 3kg are moving in a plane and their velocities are 1ms−1,2ms−2and3ms−1 respectively as shown . The total angular momentum of the system of three balls about point P at the given instant of time is
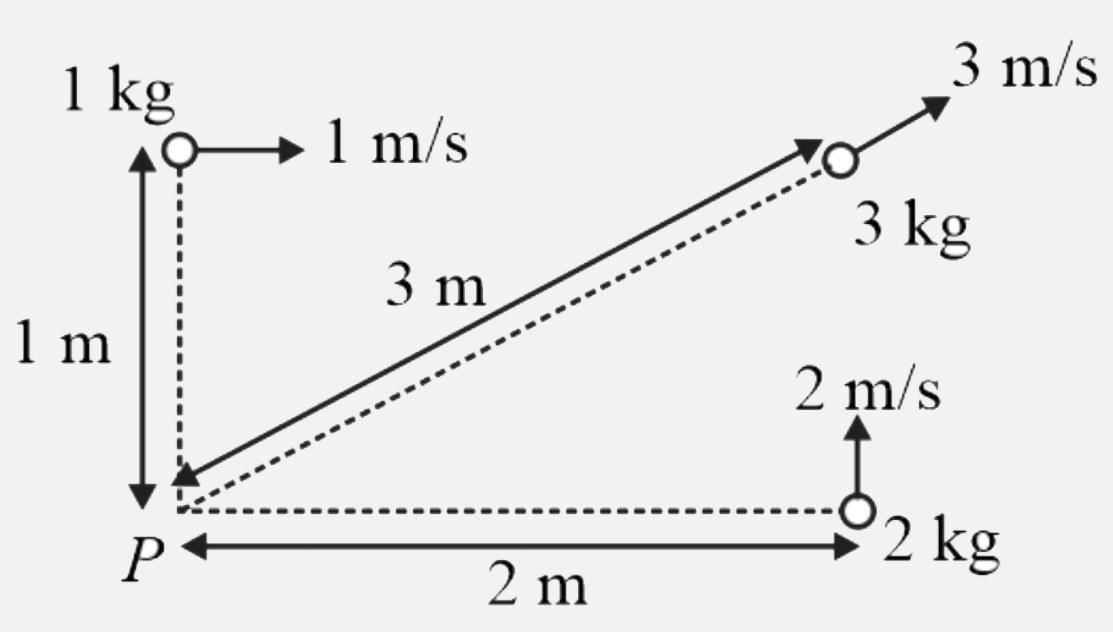
View SolutionTwo particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
View SolutionTwo objects of masses 100g and 200g are moving along the same line in the same direction with velocities of 2m/s and 1m/s, respectively. They collide and after the collison, the first object moves at a velocity of 1.67m/s in the same direction. Determine the velocity of the second object.
View SolutionA particle travels half the distance with a velocity of 6ms–1. The remaining half distance is covered with a velocity of 4ms–1 for half the time and with a velocity of 8ms–1 for the rest of the half time. What is the velocity of the particle averaged over the whole time of motion ?
View SolutionA body oa mass M at rest explodes into three pieces, two of which of mass (M/4) each are thrown- off in perpendicular directions with velocities of 6ms−1 and 8ms−1 respectively. The third piece will be thrown-off with a velocity of
View Solution
