Two charges +qand−q, each of mass m, are revoloving in a circle of radius R, under mutal electrostatic force, Find (i) speed of each charge (ii) kinitic energy of the system (iii) potental energy of the system and (iv) total energy of the system.
The charges +qand−q revolve around their center of mass O with same angular velocity. As their mass is same, their speed (v) will be same as shown in Fig.
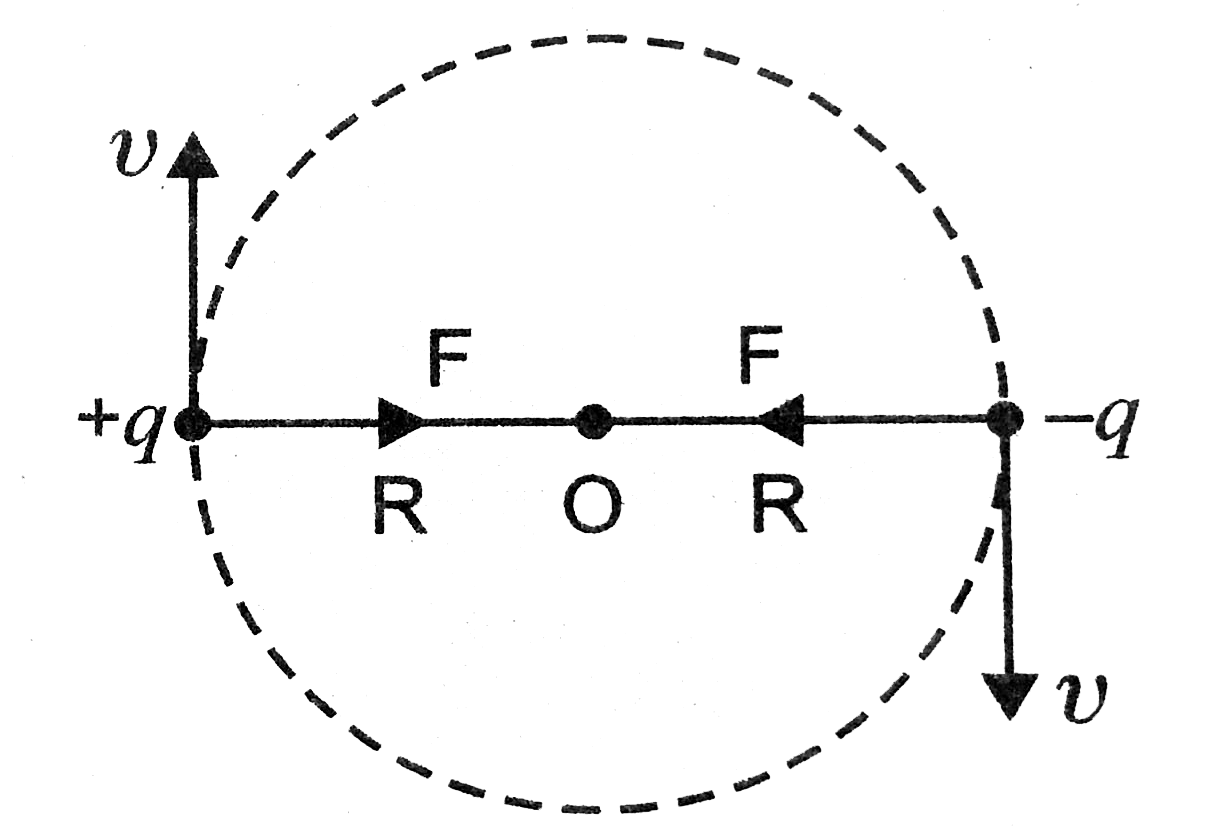
(i) The centripetal force required is provided by the electrostatic force of attraction between the two particles.
∴mv2R=14π∈0q×qR+R2
v=√q216π∈0mR
(ii) Kinectic energy of the system of two particles
K=2×12mv2=mv2=m×q216π∈0mR=q216π∈0R
(iii) Potential energy of the system
U=q(−q)4π∈0(R+R)=q28π∈0R
(iv) Total energy of the system
E=K+U=q216π∈0R−q28π∈0R
E=q216π∈0R
Similar Questions
Two charges +qand−q, each of mass m, are revoloving in a circle of radius R, under mutal electrostatic force, Find (i) speed of each charge (ii) kinitic energy of the system (iii) potental energy of the system and (iv) total energy of the system.
View SolutionFind the electric potential energy of the system of charges.
(a)
View Solution
Knowledge Check
A particle of mass m and charge -q circulates around a fixed charge q in a circle radius under electrostatic force. The total energy of the system is (k= (14πε0))
A−Kq22rBKq2rC−Kq2rDZeroAn electron of mass m and charge -e moves in circular orbit of radius r round the nucleus of charge +Ze in unielectron system. In CGS system the potential energy of electron is
A+Ze2r2B−Ze2rCZe22rD−Ze22rWhen we bring two electrons close to each other, the electrostatic potential energy of the system:
AIncreasesBBecomes zeroCRemains unchangedDDecreases
If Q charge is given to a sphere of radius R, the energy of the system is
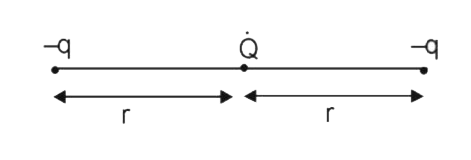
View SolutionThree charges are placed as shown in fig if the electric potential energy of system is zero, then Q : q-
View SolutionIn a solid uniformly charged sphere of total charge Q and radius R, if energy stored out side the sphere is U0 joules then find out self energy of sphere in term of U0 ?
View SolutionA uniformly charged sphere has charge Q. An electron (charge – e, mass m) revolves around it in a circular orbit of radius r. (a) Write the total energy (i.e., sum of its kinetic energy and electrostatic potential energy in the field of the sphere) of the electron. (b) If the time period of revolution of the electron in circular orbit of radius r is T, then find the time period if the orbital radius is made 4r.
View SolutionWhat do you understand by electrostatic potential energy ? Find an expression for electrostatic potential energy of a system of two point charges.
View Solution
