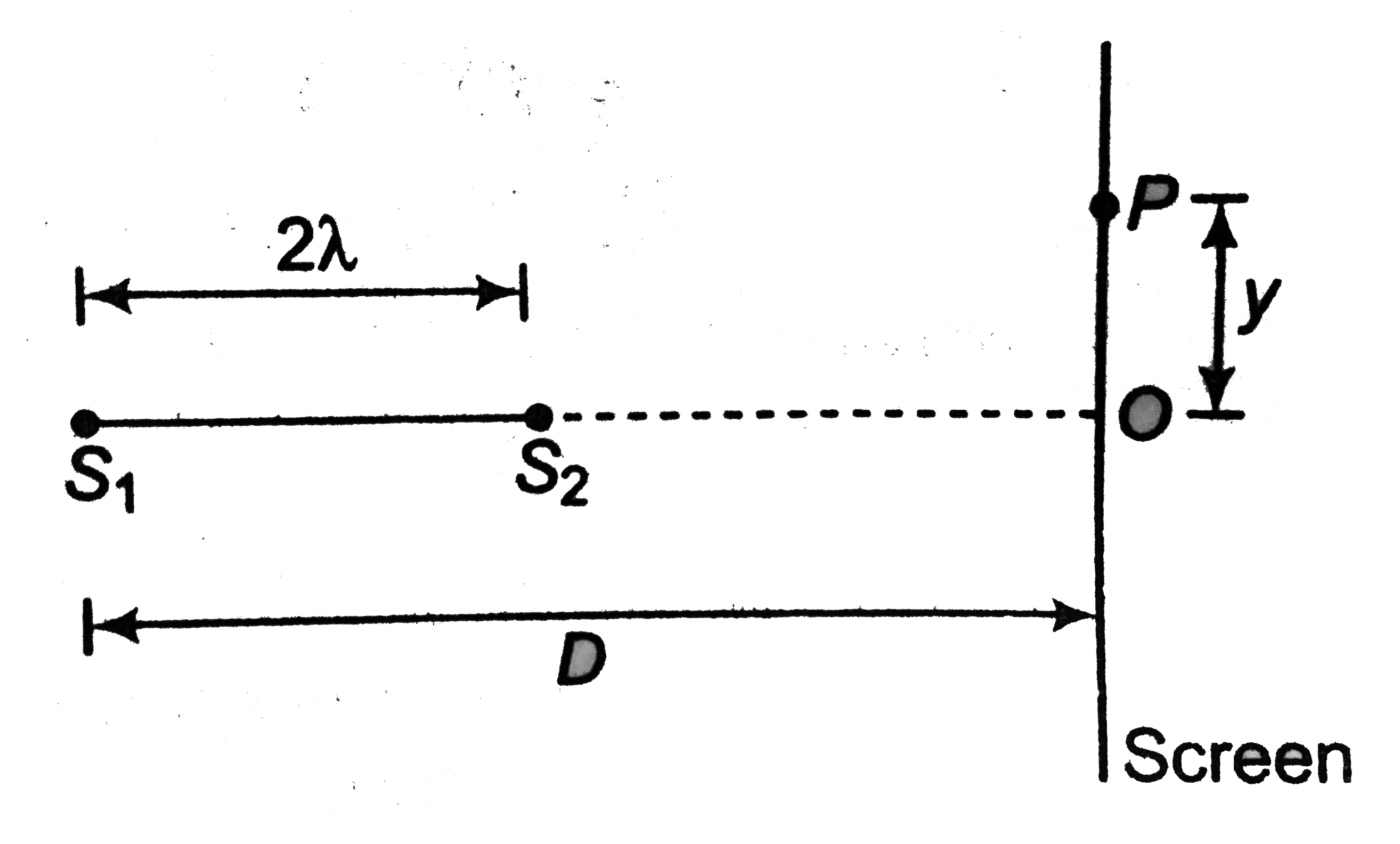
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallet to each other at a small separation of 2λ . The sound is delected by maving a delector on the screen at a distance D(>>λ) from the slit S1 as shows in figure. Find the distance y such that the intensity at P is equal to intensity at O .
The correct Answer is:C, D
Since S1,S2 are in same phase at O there wil be maximum intensity.
Given that there will be a maximum intensity at P.
→pathd⇔erence=△x=nl

From the ure (in question)
(S1P)2−(S2P)2
=(sqrtD^2+x_2)^2-[(sqrtD-2lamda^2+x^2]^2<br>=4lamdaD=4lamda^2=4lamdaD<br>(lamda^2issosmallandcan²cted)<br>S_1P-S_2P=(4lamdaD)/(2sqrt(x^2+D^2))=nlamda<br>=(2D)/(sqrt(x^2+D^2))=n<br>rarr n^2(x^2+D^2)=4D^2<br>rarr x=D/n sqrt4-n^2<br>Whenn=1, x=sqrt3D(1st order)<br>n=2,<br>x=0 (2nd order)
∴Wenx=√3D
at P there will be maximum intensity
Topper's Solved these Questions
Similar Questions
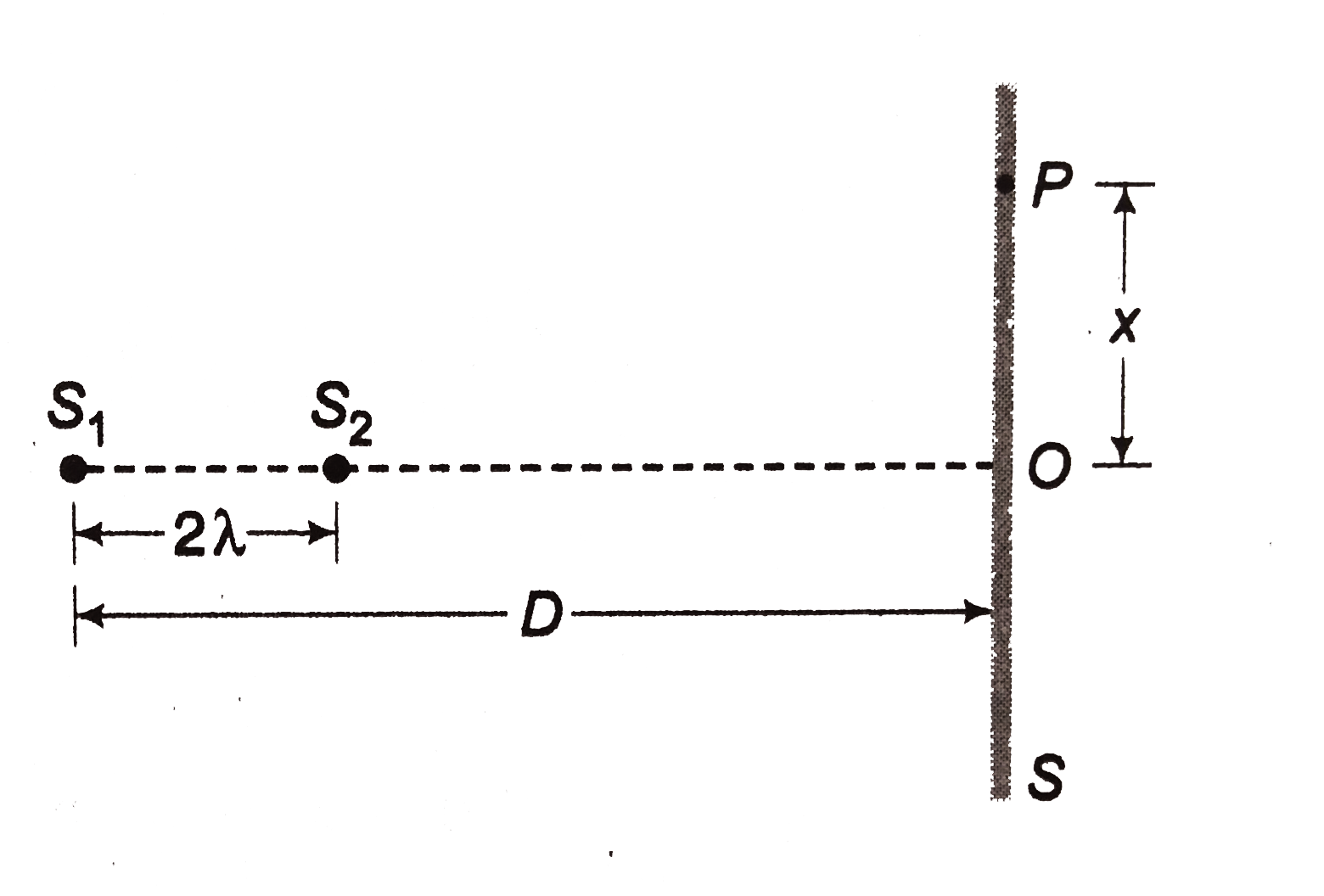
Two coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(gtgtλ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O.
 .View Solution
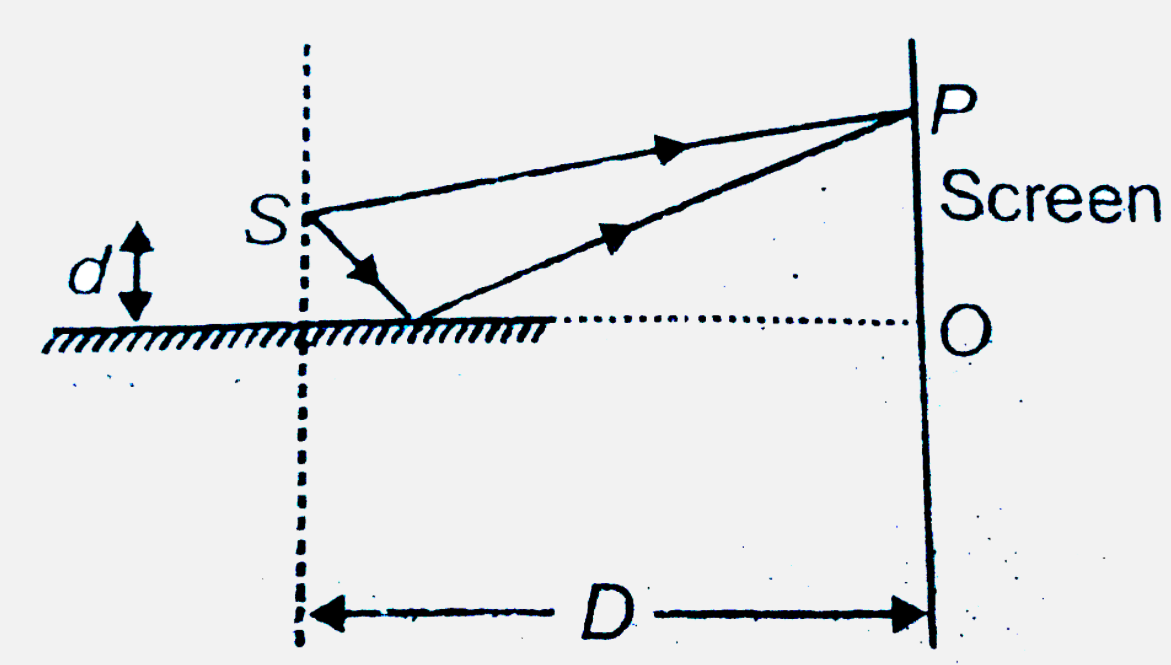
.View SolutionA narrow slit S transmitting light of wavelength 'λ'. Is placed at a distance d above a large plane mirror as shown. The light coming directly from the slit and that coming after the reflection interfere at a screen S placed at a distance D from the slit. at what distance from point O, the resultant intensity is maximum ? (there is a phase change of π of reflection from the mirror)
 View Solution
View SolutionIn a Lloyds's mirror experiment as narrow slit S transmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.
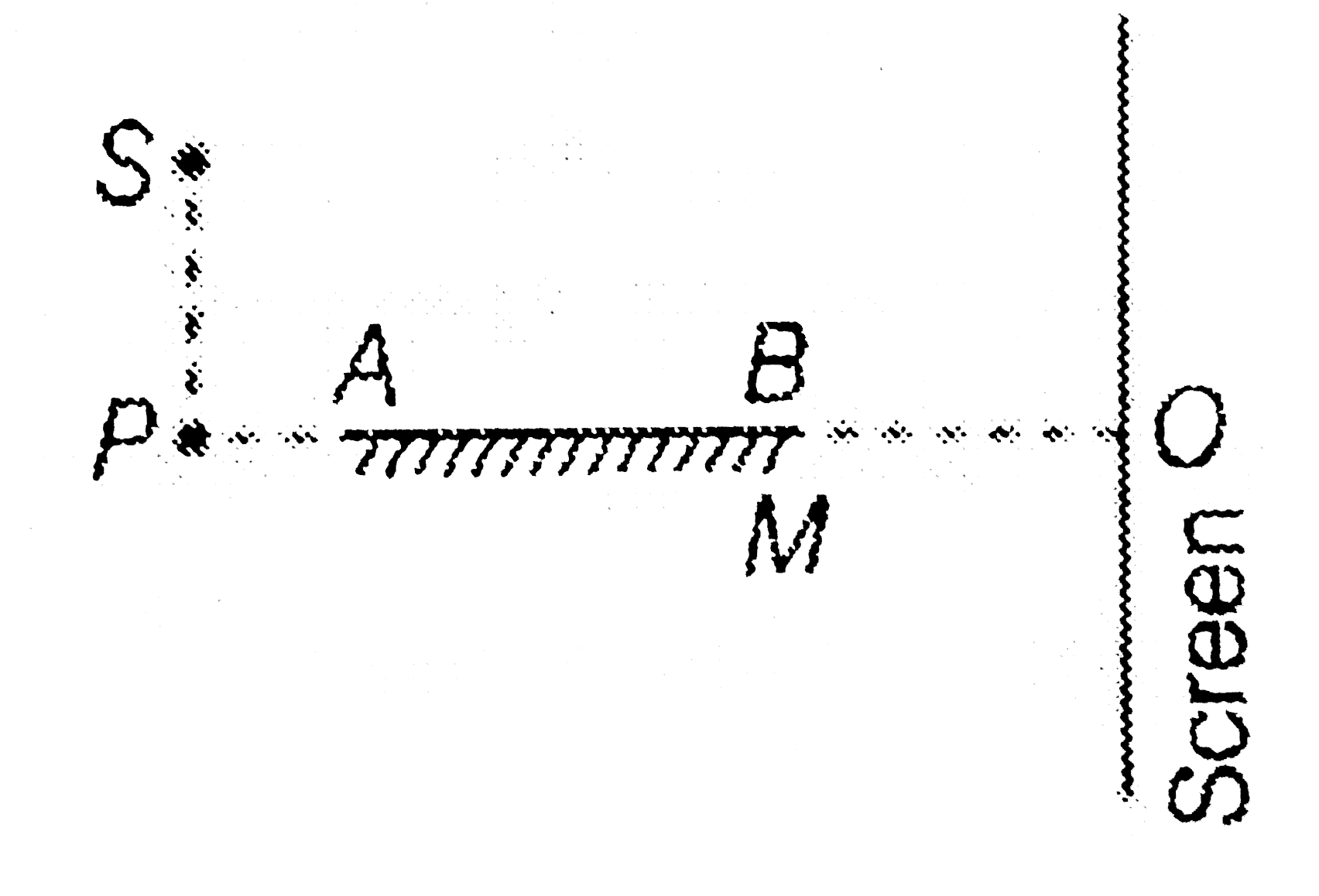
If the mirror is shifted towards left then how does the fringe pattern on screen changes ?View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between them is 2λ as shown in figure. The first bright fringe is formed at .P. due to interference on a screen placed at a distance .D. from S1 (D>>λ), then OP is
 View Solution
View SolutionThe figure shows two points source which emit light of wavelength λ in phase with each other and are at a distance d=5.5λ apart along a line which is perpendicular to a large screen at a distance L from the centre of the source. Assume that d is much less than L. Which of the following statement is (are) correct ?
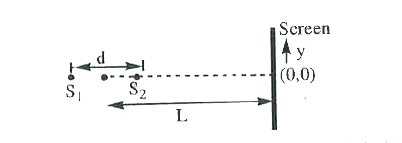 View Solution
View SolutionA narrow slit S transmitting light of wavelength λ is placed a distance d above a large plane mirror as shown in figure. The light coming directly from the slit and that coming after the reflection interference at a screen ∑ placed at a distance LD from the slit. a. What will be the intensity at a point just above the mirror. i.e., just above O? b. At what distance from O does the first maximum occur?
? View Solution
View Solution2 loudspeakers are emitting sound waves of wavelength lambda with an initial phase difference of π2 at what minimum distance from O on line AB will one hear a maximum
 View Solution
View SolutionIn a young's doule slits experiment, a monochromatic source of wavelength λ is used to illuminate the two slits
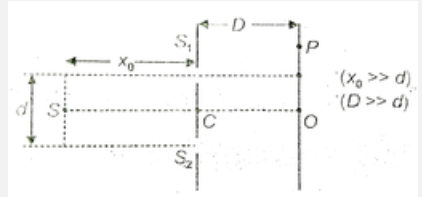
S1 and S2. The slitss S1 and S2 are identical and source S is placed symmetrically as shown. interference pattern is observed on a screen at a distance D from the centre of slit. The distance between the slits is d.
If the resultant intensity at P is same as that O, then the distance OP can not beView SolutionConsider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
View SolutionA coherent parallel beam of microwaves of wavelength λ=0.5mm falls on aYoung's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in figure
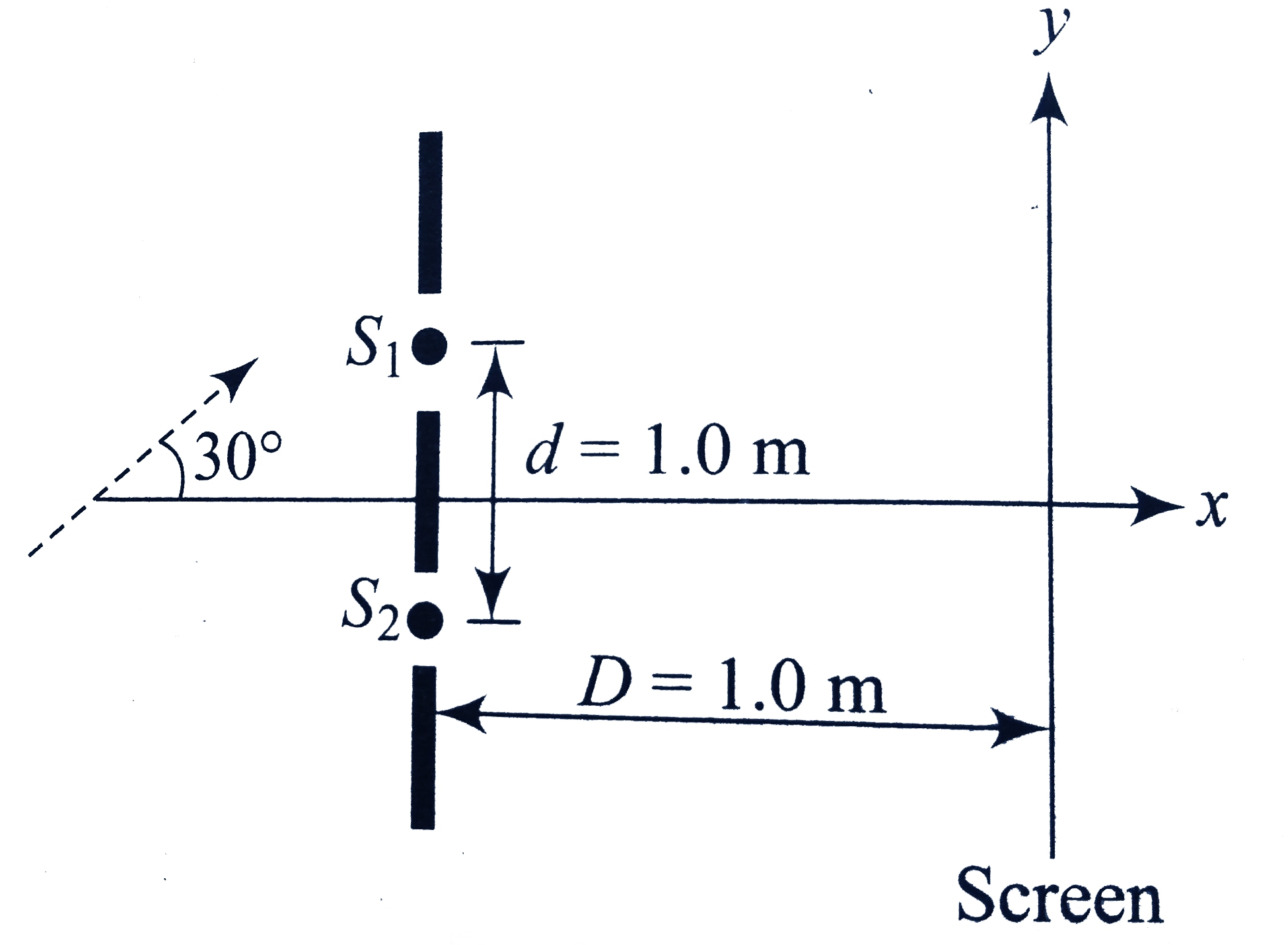
If the incient beam falls normally on the double-slit apparatus, find the order of the interference minima on the screenView Solution

