Two coherent sources A and B of radio waves are 5.00 m apart. Each source emits waves with wavelength 6.00m. Consider points along the line between the two sources. At what distances, if any, from A is the interference (a) constructive (b) destructive?
To solve the problem of finding the distances from source A where constructive and destructive interference occurs, we can follow these steps:
Step 1: Understand the setup
We have two coherent sources A and B that are 5.00 m apart, emitting waves with a wavelength of 6.00 m. We need to find points along the line between these two sources where constructive and destructive interference occurs.
Step 2: Define the conditions for interference
- Constructive interference occurs when the path difference (Δx) between the waves from the two sources is an integer multiple of the wavelength (λ):
Δx=nλ(n=0,1,2,…)
- Destructive interference occurs when the path difference is an odd multiple of half the wavelength:
Δx=(n+12)λ(n=0,1,2,…)
Step 3: Set up the path difference
Let x be the distance from source A to a point P along the line between A and B. The distance from B to point P will then be 5−x.
The path difference is given by:
Δx=|(5−x)−x|=|5−2x|
Step 4: Find conditions for constructive interference
For constructive interference:
|5−2x|=n⋅6
This gives two cases:
1. 5−2x=n⋅6
2. 2x−5=n⋅6
Case 1:
5−2x=n⋅6⟹2x=5−n⋅6⟹x=5−n⋅62
Case 2:
2x−5=n⋅6⟹2x=n⋅6+5⟹x=n⋅6+52
Step 5: Analyze the cases for constructive interference
For n=0:
- From Case 1: x=52=2.5m
- From Case 2: x=52=2.5m
For n=1:
- From Case 1: x=5−62=−0.5m (not valid)
- From Case 2: x=6+52=5.5m (not valid)
For n=2:
- From Case 1: x=5−122=−3.5m (not valid)
- From Case 2: x=12+52=8.5m (not valid)
Thus, the only valid point for constructive interference is at x=2.5m.
Step 6: Find conditions for destructive interference
For destructive interference:
|5−2x|=(n+12)⋅6
This gives two cases:
1. 5−2x=(n+12)⋅6
2. 2x−5=(n+12)⋅6
Case 1:
5−2x=(n+12)⋅6⟹2x=5−(n+12)⋅6⟹x=5−(n+12)⋅62
Case 2:
2x−5=(n+12)⋅6⟹2x=(n+12)⋅6+5⟹x=(n+12)⋅6+52
Step 7: Analyze the cases for destructive interference
For n=0:
- From Case 1: x=5−32=1m
- From Case 2: x=3+52=4m
For n=1:
- From Case 1: x=5−92=−2m (not valid)
- From Case 2: x=9+52=7m (not valid)
Thus, valid points for destructive interference are at x=1m and x=4m.
Final Answers
- Constructive interference occurs at: x=2.5m
- Destructive interference occurs at: x=1m and x=4m
We have two coherent sources A and B that are 5.00 m apart, emitting waves with a wavelength of 6.00 m. We need to find points along the line between these two sources where constructive and destructive interference occurs.
- Constructive interference occurs when the path difference (Δx) between the waves from the two sources is an integer multiple of the wavelength (λ):
Δx=nλ(n=0,1,2,…)
- Destructive interference occurs when the path difference is an odd multiple of half the wavelength:
Δx=(n+12)λ(n=0,1,2,…)
Let x be the distance from source A to a point P along the line between A and B. The distance from B to point P will then be 5−x.
Δx=|(5−x)−x|=|5−2x|
For constructive interference:
|5−2x|=n⋅6
This gives two cases:
1. 5−2x=n⋅6
2. 2x−5=n⋅6
5−2x=n⋅6⟹2x=5−n⋅6⟹x=5−n⋅62
2x−5=n⋅6⟹2x=n⋅6+5⟹x=n⋅6+52
For n=0:
- From Case 1: x=52=2.5m
- From Case 2: x=52=2.5m
- From Case 1: x=5−62=−0.5m (not valid)
- From Case 2: x=6+52=5.5m (not valid)
- From Case 1: x=5−122=−3.5m (not valid)
- From Case 2: x=12+52=8.5m (not valid)
For destructive interference:
|5−2x|=(n+12)⋅6
This gives two cases:
1. 5−2x=(n+12)⋅6
2. 2x−5=(n+12)⋅6
5−2x=(n+12)⋅6⟹2x=5−(n+12)⋅6⟹x=5−(n+12)⋅62
2x−5=(n+12)⋅6⟹2x=(n+12)⋅6+5⟹x=(n+12)⋅6+52
For n=0:
- From Case 1: x=5−32=1m
- From Case 2: x=3+52=4m
- From Case 1: x=5−92=−2m (not valid)
- From Case 2: x=9+52=7m (not valid)
- Constructive interference occurs at: x=2.5m
- Destructive interference occurs at: x=1m and x=4m
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Single Correct
11 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - LEVEL 2 (single correct option)
1 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1Subjective
22 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
The path length difference between two waves coming from coherent sources for destructive interference should be
View SolutionTwo coherent sources separated by distance d are radiating in phase having wavelength λ. A detector moves in a big circle around the two sources in the plane of the two sources. The angular position of n=4 interference maxima is given as

View SolutionTwo sound sources emitting sound each of wavelength λ are fixed at a given distance apart. A listener moves with a velocity u along the line joining the two sources. The number of beats heard by him per second is
View SolutionTwo coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
View SolutionTwo point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source (a) on the line joining the sources and (b) on the perpendicular bisector of the line joining the sources ?
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionA point source emits sound waves with an average power output of 80.0 W (a) Find the intensity 3.00 m from the source. (b) find the distance at which the intensity of the sound is 1.00×10−8Wm2
View SolutionTwo point sound sources A and B each to power 25πw and frequency 850Hz are 1m apart. The sources are in phase
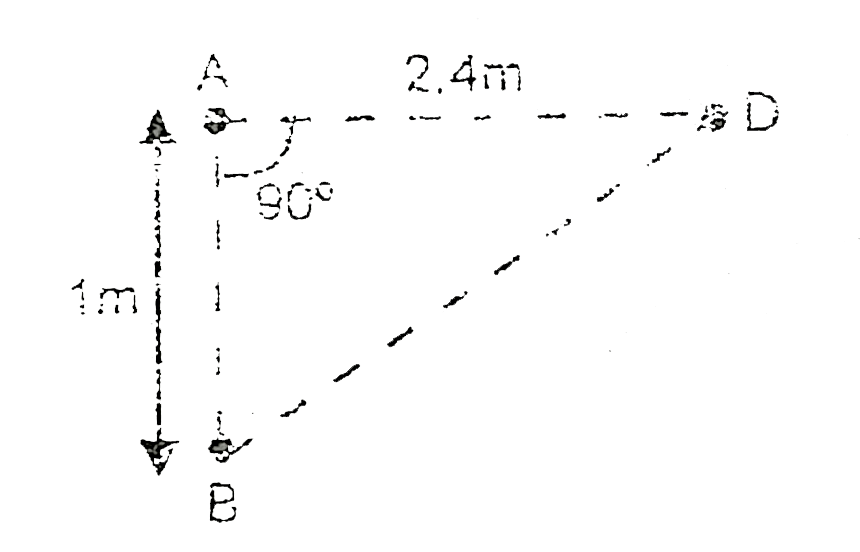
Determine the phase difference between the waves emitting from A and B received by detector D as shown in figure. Velocity of sound =340m/s.
View SolutionLight waves of wavelength 5460 A, emitted by two coherent sources, meet at a point after travelling different paths. The path difference between the two wave trains at that point is 2.1μm. then phase difference will be ?
View SolutionTwo coherent point sources S1andS2 emit light of wavelength λ. The separation between sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance on this line from S2 where a minimum of intensity occurs?
View Solution
