Two convex lenses of focal length and respectively placed coaxially and are separated by some distance d. The whole system behaves like a concave lens. One of the possible value of d is
The correct Answer is:B
To solve the problem of two convex lenses behaving like a concave lens when placed coaxially and separated by a distance d, we can follow these steps:
1. Identify the Focal Lengths:
- Let the focal length of the first lens f1=+10cm (convex lens).
- Let the focal length of the second lens f2=+20cm (convex lens).
2. Understand the Equivalent Focal Length:
- When two lenses are placed in combination, the equivalent focal length F can be calculated using the formula:
1F=1f1+1f2−df1f2
- Here, d is the distance between the two lenses.
3. Condition for Concave Lens:
- For the system to behave like a concave lens, the equivalent focal length F must be negative:
F<0
4. Set Up the Inequality:
- From the formula, we can rearrange it to find the condition for d:
1F=1f1+1f2−df1f2<0
- This implies:
df1f2>1f1+1f2
5. Calculate the Right Side:
- Find 1f1+1f2:
1f1=110=0.1cm−1
1f2=120=0.05cm−1
1f1+1f2=0.1+0.05=0.15cm−1
6. Calculate f1f2:
- Multiply the focal lengths:
f1f2=10×20=200cm2
7. Set Up the Final Inequality:
- Substitute into the inequality:
d>f1f2⋅(0.15)
d>200⋅0.15=30cm
8. Conclusion:
- Therefore, one possible value of d must be greater than 30cm. If we check the options, d=40cm is a valid choice.
Final Answer:
One of the possible values of d is 40cm.
---
- Let the focal length of the first lens f1=+10cm (convex lens).
- Let the focal length of the second lens f2=+20cm (convex lens).
- When two lenses are placed in combination, the equivalent focal length F can be calculated using the formula:
1F=1f1+1f2−df1f2
- Here, d is the distance between the two lenses.
- For the system to behave like a concave lens, the equivalent focal length F must be negative:
F<0
- From the formula, we can rearrange it to find the condition for d:
1F=1f1+1f2−df1f2<0
- This implies:
df1f2>1f1+1f2
- Find 1f1+1f2:
1f1=110=0.1cm−1
1f2=120=0.05cm−1
1f1+1f2=0.1+0.05=0.15cm−1
- Multiply the focal lengths:
f1f2=10×20=200cm2
- Substitute into the inequality:
d>f1f2⋅(0.15)
d>200⋅0.15=30cm
- Therefore, one possible value of d must be greater than 30cm. If we check the options, d=40cm is a valid choice.
One of the possible values of d is 40cm.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Subjective
29 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Assertion And Reason
13 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
Two plano-convex lenses of focal lengths 20cm and 30cm are placed together to form a double convex lens. The final focal length will be
View SolutionTwo converging lenses of focal lengths f1=10cm and f2=20cm are placed at some separation. A parallel beam of light is incident on first lens. Then,
View SolutionA convex lens of focal length 100 cm and a concave lens of focal length 10 cm are placed coaxialiy at a separation of 90 cm. If a parallel beam of light is incident on convex lens, then after passing through the two lenses the beam
View SolutionA convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 20 cm apart. In between them an object placed at distance x from the convex lens.
What is the value of x (in cm ) so that images from by both the lenses coincides ?
View SolutionA convex lens of focal length 20cm and a concave lens of focal length f are mounted coaxially 5cm apart. Parallel beam of light incident on the convex lens emerges from the concave lens as a parallel beam. Then, f in cm is
View SolutionA convex lens of focal length 10 cm and a concave lens of same focal length in value are placed co-axially at a separation of 20 cm as shown in figure. A point object is at infinity on the principal axis. Take the optic center of convex lens as origin of co ordinate system and the principal axis as x-axis as shown in figure.
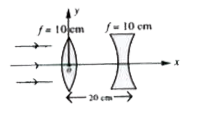
In the initial positin (as given in the passage ) if the concave lens has a velocit of 9 cm/s towards the convex lens, the velocity of the final image will be
View SolutionA convex lens of focal length 10 cm and a concave lens of same focal length in value are placed co-axially at a separation of 20 cm as shown in figure. A point object is at infinity on the principal axis. Take the optic center of convex lens as origin of co ordinate system and the principal axis as x-axis as shown in figure.

The co-ordinates of the image formed after refraction through both the lenses is
View SolutionTwo convex lenses f focal length 20 cm each are placed coaxially with a separation of 60 cm between them. find the image of a distance object formed by the combination by a. using thin les formula separately for the two lenses and b. using the equivalent lens. Note that although the combination forms a real image of as distance object on the other side, it is equivalent to as diverging lens as far as the locatiion of the final image is concerned.
View SolutionA convex lens of focal length 20cm and another plano convex lens of focal length 40cm are placed co-axially . The plano convex lens is silvered on plane surface. What should be the distance (in cm) so that final image of the object 'O' is formed on O itself.
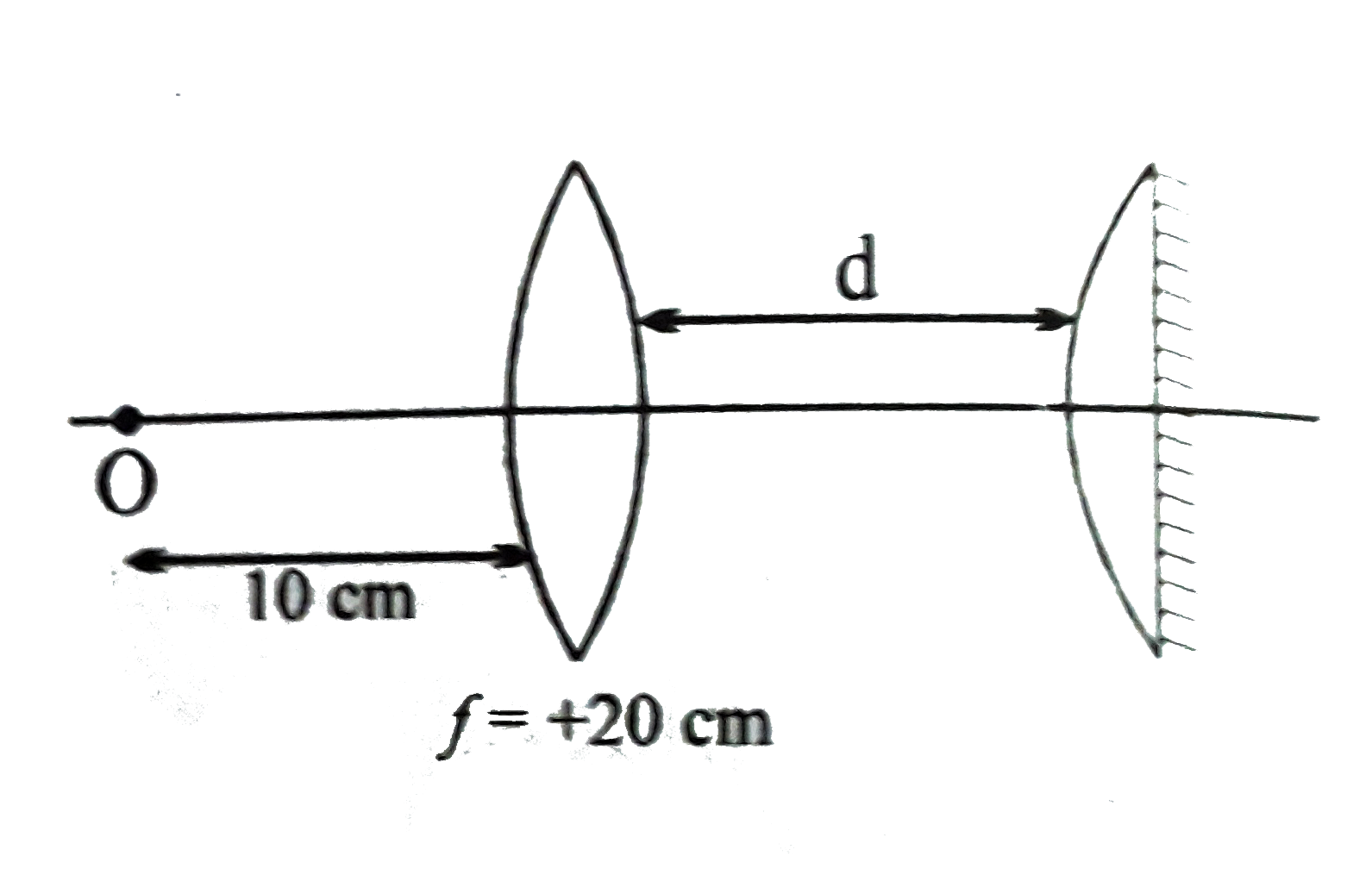
View SolutionTwo thin lenses of focal lengths 20 cm and -20 cm are placed in contact with other. The combination has a focal length equal to
View Solution
