Two equal positive charges, each of $2 μ C$ interact with a third positive charge of $3 μ C$ situated as shown in Fig. Calculate the magnitude and direction of the force on the $3 μ C$ charge.

Video Solution

Text Solution

Verified by Experts

In fig ,
$O A = O B = 3 m, O P = 4 m$
$∴ A P = B P = \sqrt{3^{2} + 4^{2}} = 5 m$
According to Coulomb's law,
Force on charge at P due to charge at A
$F_{1} = \frac{1}{4 π \in_{0}} \frac{q_{1} q_{2}}{{(A P)}^{2}}$
$F_{1} = \frac{9 \times 10^{9} \times (2 \times 10^{- 6}) \times (3 \times 10^{- 6})}{5^{2}}$
$= \frac{54}{25} \times 10^{- 3} N = 2.16 \times 10^{- 3} N$
$F_{1} = 2.16 X X 10^{- 3} N$ , along $P A'$ opposite to $P A$ . It has two recentangular components $F_{2} cos 0$ along $P X$ and $F_{1}$ sin 0 along $P Y'$ . Similarly, force on charge along $P B$ opposite to $P B'$ . It also has two recentangular components : $F_{2} cos 0$ along $P X$ and $F_{2} sin 0$ along $P Y$ .
The components along $P Y'$ cancel. The components along $P X$ add up.
Total force on $3 μ C$ charge is $F = 2 F_{1} cos θ$
$= 2 \times 2.16 \times 10 \times 10^{- 3} \times \frac{4}{5}$
$= 3.5 \times 10^{- 3} N$ , along PX.

Updated on:21/07/2023

Two charges each of $1 μ C$ are at 3 cm. Then the force between them is
A100 N
B10 N
C $10^{4}$ dyne
D1000 N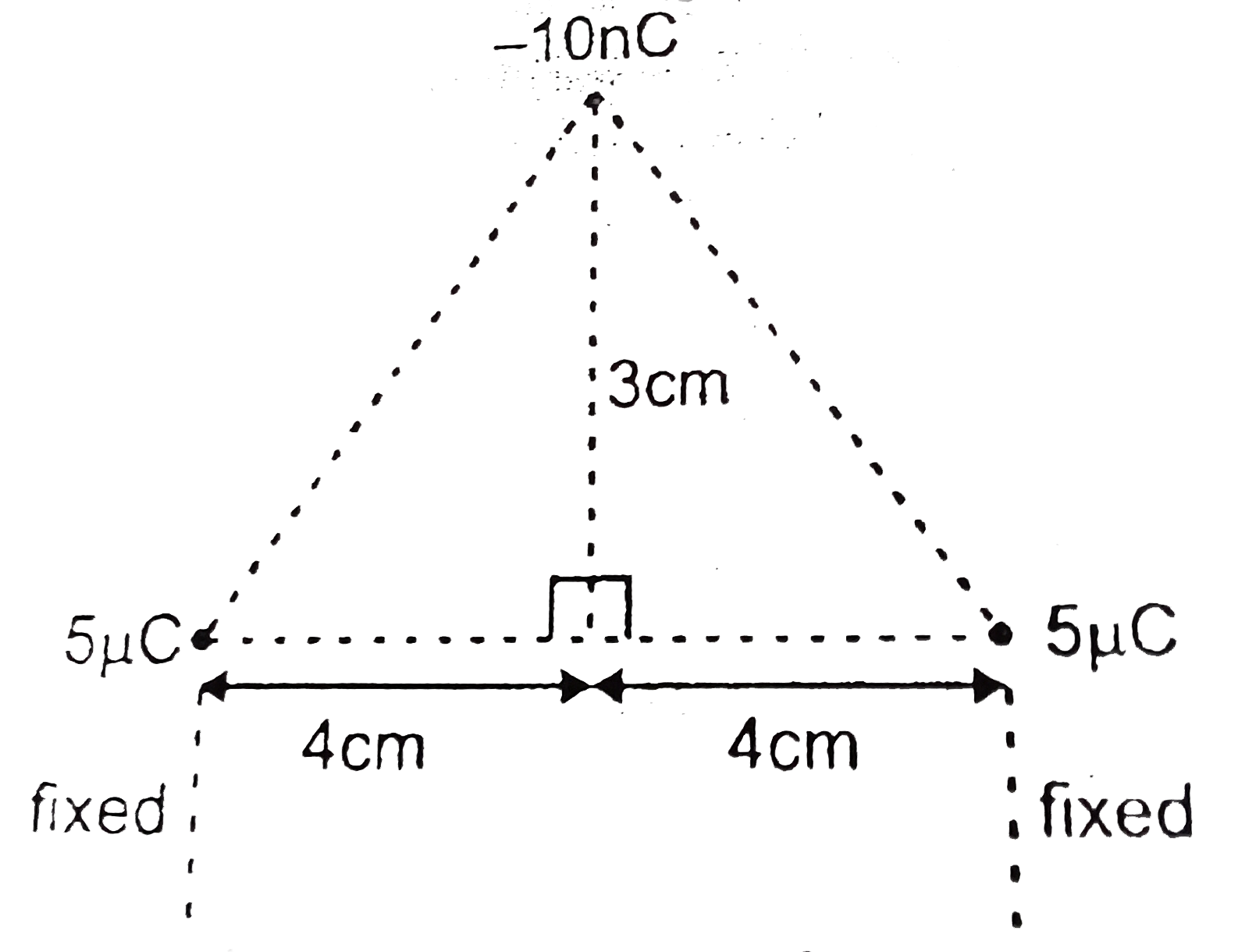
Figure shows two fixed positive point charges of magnitude $5 μ C$ A negative point charge of $- 10 n C$ and mass $1 k g$ is released as shown in figure (consider only electrostatic foces)
AInitial acceleration fo $- 10 n C$ charge is $0.216 m / s^{2}$
Binitial acceleration of $- 10 n C$ charge is $2.16 m / s^{2}$
CKinetic energy of $- 10 n C$ charge when it crosses the line joining two fixed charges is 4.5 mJ
DKinetic energy of $- 10 n C$ charge when it crosses the line joining two fixed charges is 3 mJ.