Two identical buggies 1 and 2 with one man in each move along parallel rails. When the buggies are opposite to each other, the men jump in a direction perpendicular to the direction of motion of buggies, so as to exchange their places. As a consequence, buggy 1 stops and buggy 2 keeps moving in the same direction with its final velocity v. Find the initial velocities v1 and v2 of buggies. Mass of each buggy (without man) equals M mass of each man is ignore frictional effects anywhere and the buggies are constrained to move along the rails only.
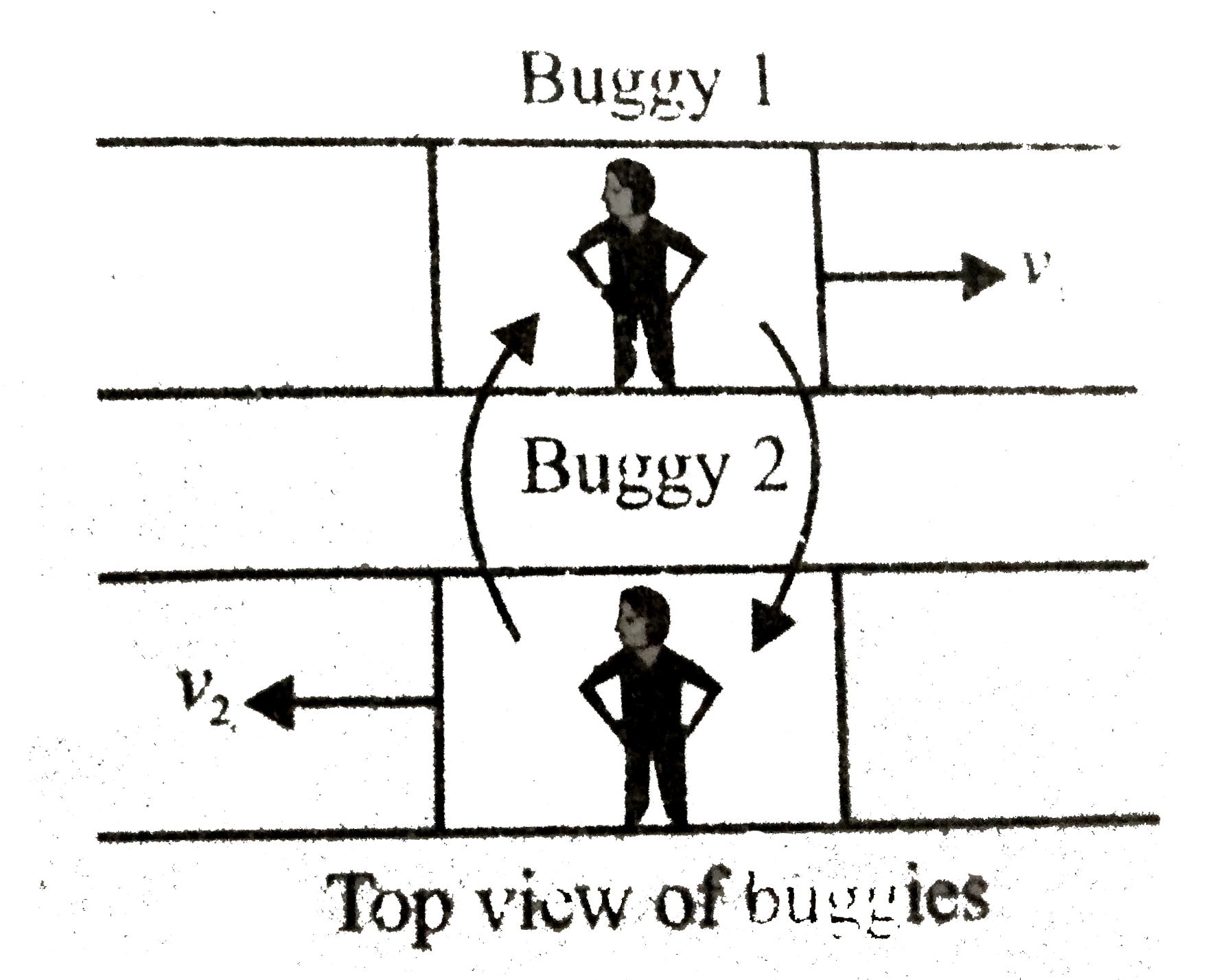
In the problems involving mass ejection and mass addtions, the ejected and added mass both are part of a system. When the men jump they push on the floor of the bugy (action), the same force acts on them as well (reaction).
This action reaction pair is intenal force for the system of man and buggy. similarly, when men jump in, there is an action reaction force between them and the buggy.
Let buggy 1 moves to the right and buggy 2 to the left, when the men jump. Man in 1 brings momentum mv1 directed towards right in buggy 2.
similarly, the main 2 brings momentum mv2 in 2 directed towards left.
for system 1:
Pi(M+m)v1−mv1−v2=Mv1−mv2
Pf=0
Form law of conservation of momentum.
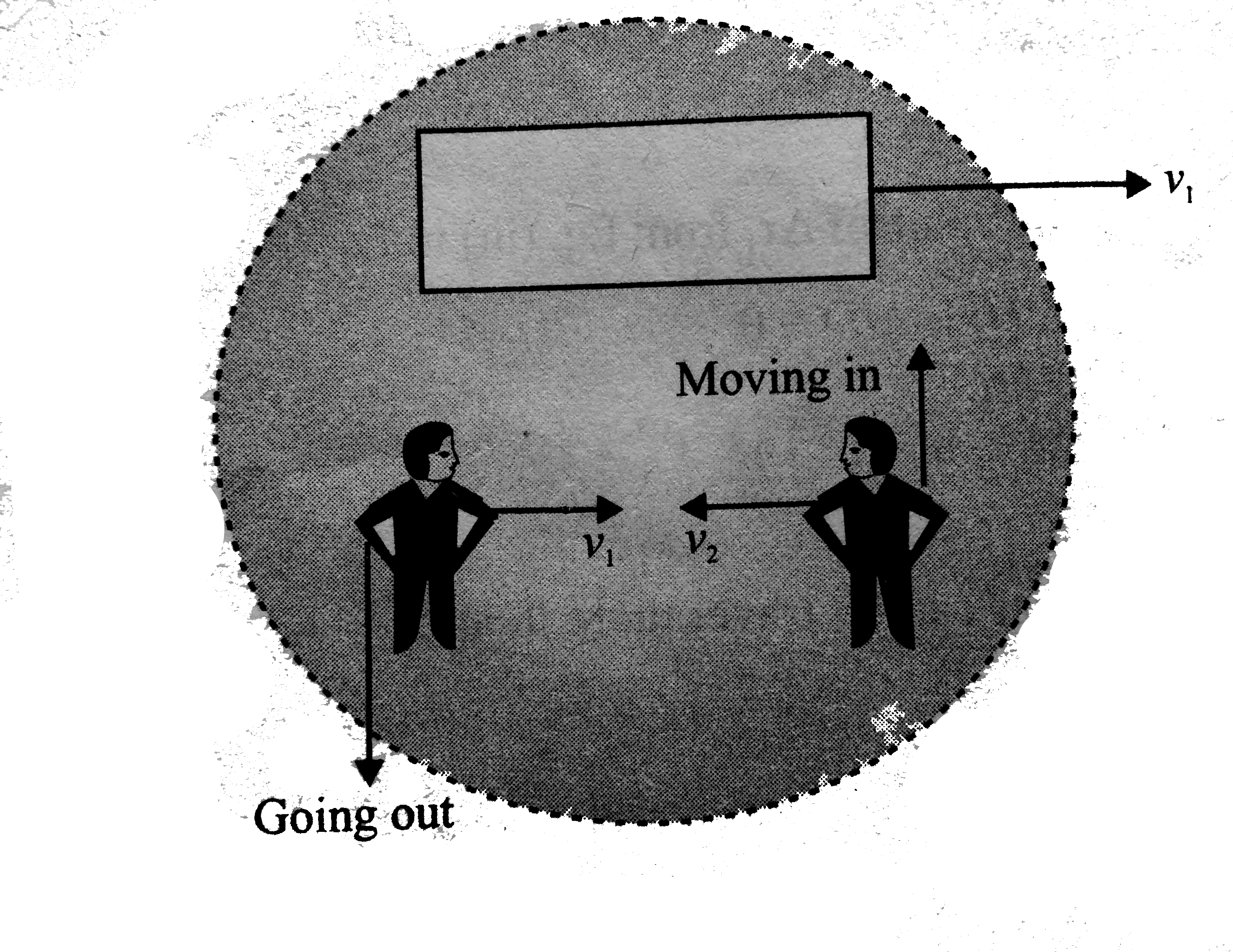
P1=Pf
Mv1=mv2=0.............i
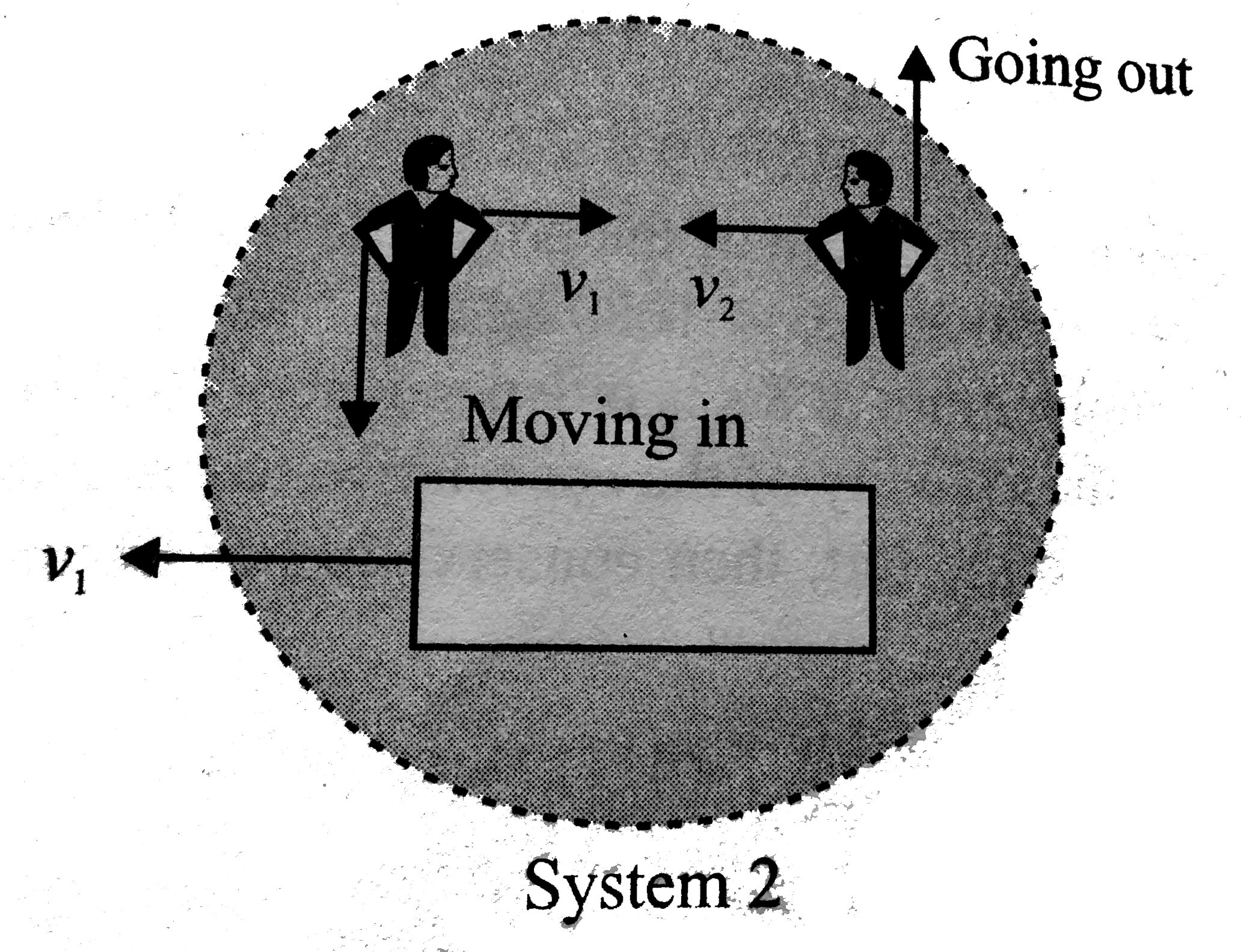
For system 2:
Pi=(M+m)v2−mv1−mv2
Pf=(M+m)v
Pi=Pf.............ii
(Mm)v2−mv1−mv2=(M+m)v..........ii
On solving eqn i and ii simultaneouysly we obtain v1=mv(M−m),v2=Mv(M−m)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Two identical buggies 1 and 2 with one man in each move without friction due to inertia along the parallel rails toward each other. When the buggies get opposite each other, the men exchange their places by jumping in the direction perpendicular to the motion direction. As a consequence, buggy 1 stops and buggy 2 keeps moving in the same direction, with its velocity becoming equal to v. Find the initial velocities of the buggies v1 and v2 if the mass of each buggy (without a man) equals M and the mass of each man m.
View SolutionTwo particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.

View Solution
Knowledge Check
Two particles of mass m and 2 m moving in opposite directions collide elastically with velocities v and 2v. Find their velocities after collision.
A0, 3vB1, 3vC0, 1vD0, 4vA mass m moves with a velocity v and collides inelastically with another identical mass. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision
AvB√3vC2√3vDv√3
Two particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.

View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionA mass m moves with a velocity v and collides inelastically with another identical mass. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision
View SolutionShows a wire sliding on two parallel, conducting rails placed at a separaton l. A magnetic feld B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constatn velocity v ?

View Solution
