Two inclined planes OA and OB having inclination (with horizontal) 30∘ and 60∘(with horizontal), respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10√3ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
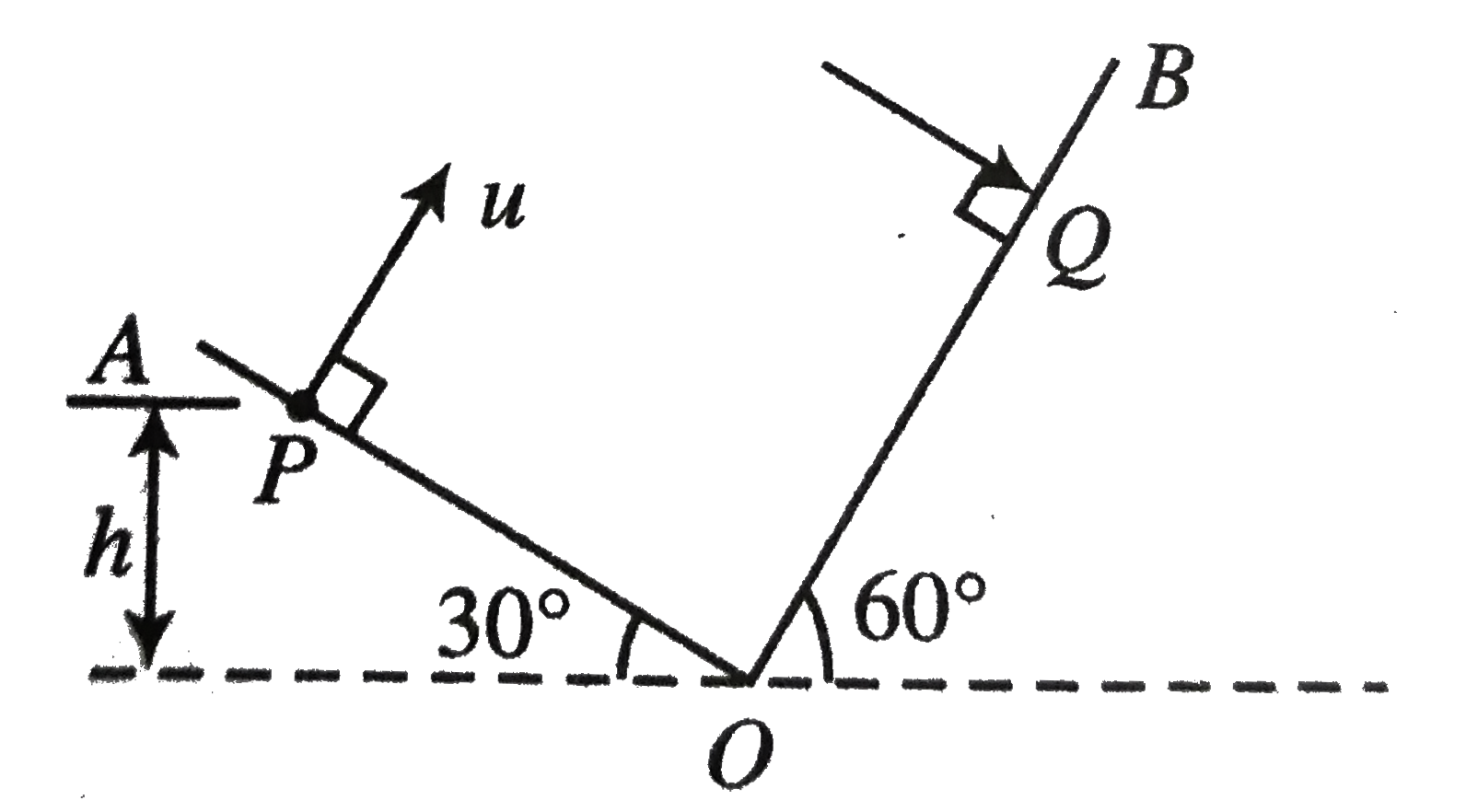
The maximum height attained by the particle (from the line O)
20.5 m
5 m
16.25 m
11.25 m
The correct Answer is:C
c. Two given planes are mutually perpendicular and the particle
is projected perpendicularly from plane OA. It means →u is
parallel to plane OB.
At the instant of collision of the particle with OB, its velocity
is perpendicular to OB or velocity component parallel to OB
is zero.
First considering motion of particle parallel to plane OB,
u=10(√3)ms−1,
Acceleration =−gsin60∘=−5√3ms−2
v=0,t=?s=?
Using v=u+at⇒0=10√3−5√3t⇒t=2s.
s=ut+12at2⇒OQ=10√3×2−125√3(2)2
⇒OQ=10(√3)m.
Now considering motion of the particle normal to plane OB.
Initial, velocity = 0, acceleration =gcos60∘=5ms−2
t=2s,v=?s=PQ=?
Using v=u+at,we≥tv=10ms−1
s=it+12at2orPO=10m
h=POsin30∘=10×sin30∘=5,
Inclination of velocity at point P with the vertical is 30∘.
therefore its vertical component is ,
ucos30∘=15ms−1upwards
Considering vertically upward motion of the particle from P.
Initial velocity =15ms−1,
Acceleration =−g=−10ms−2,v=0,s=H=?
Using v2=u2+2as, we get H=11.25m
Maximum height reached by particle above O is
h + H = 16.25m
Distance PQ=√(PO)2+(OQ)2=√(102)+(10√3)2=20m .
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Integer Type
17 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Fill in the blanks
4 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type
26 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Two inclined planes OA and OB having inclination (with horizontal) 30∘and60∘, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10√3ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate
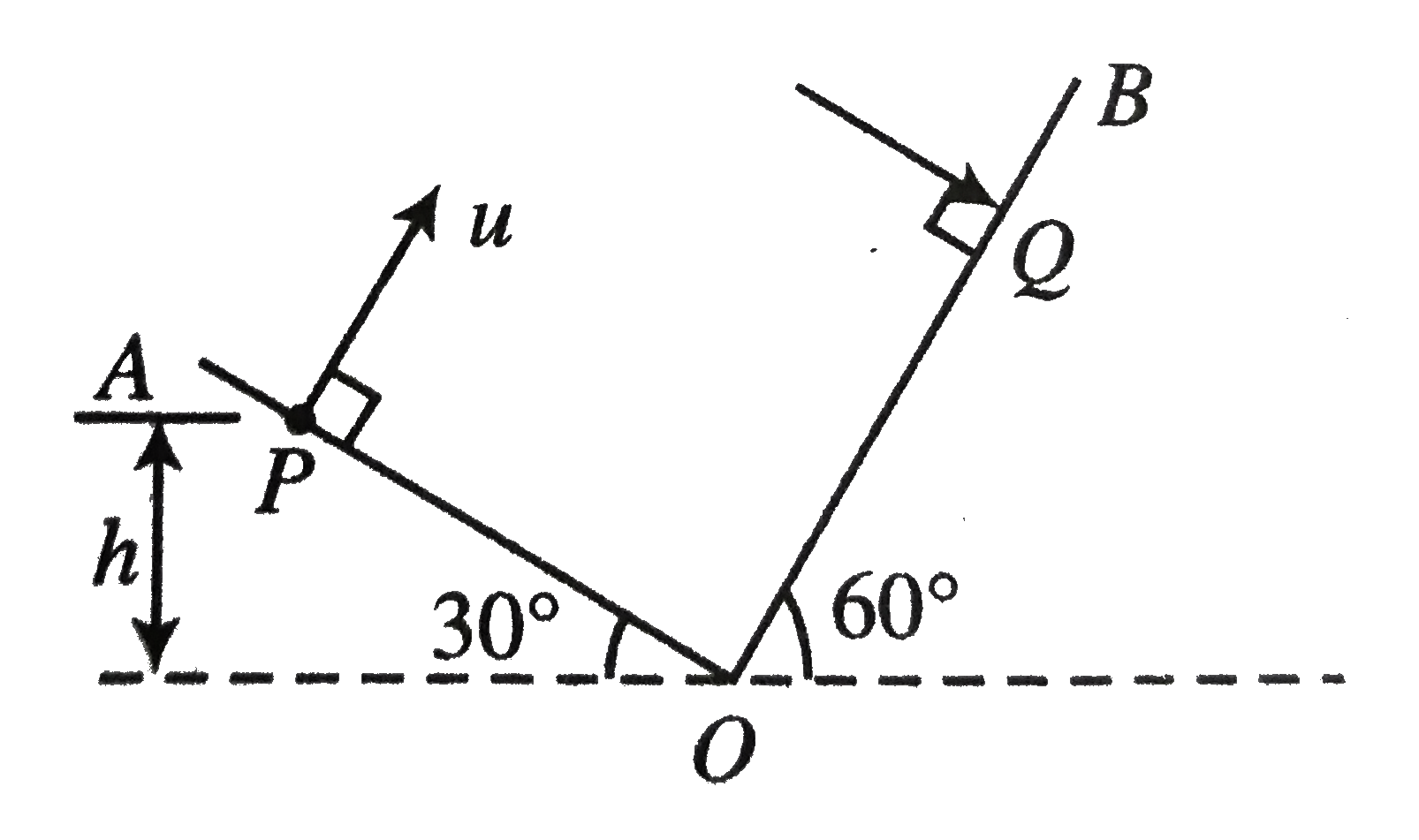
The vertical height h of P from O,
View SolutionTwo inclined planes OA and OB having inclination (with horizontal) 30∘ and 60∘, respectively, intersect each other at O as shown in figure. A particle is projected from point P with velocity u=10(√3)ms−1 along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicularly at Q, calculate

The velocity with which particle strikes the plane OB,
View SolutionTwo inclined planes OA and OB having inclinations 30∘ and 60∘ with the horizontal respectively intersect each other at O, as shown in figure. A particle is projected from point P with velocity u=10√3m/s along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicular at Q. Calculate.
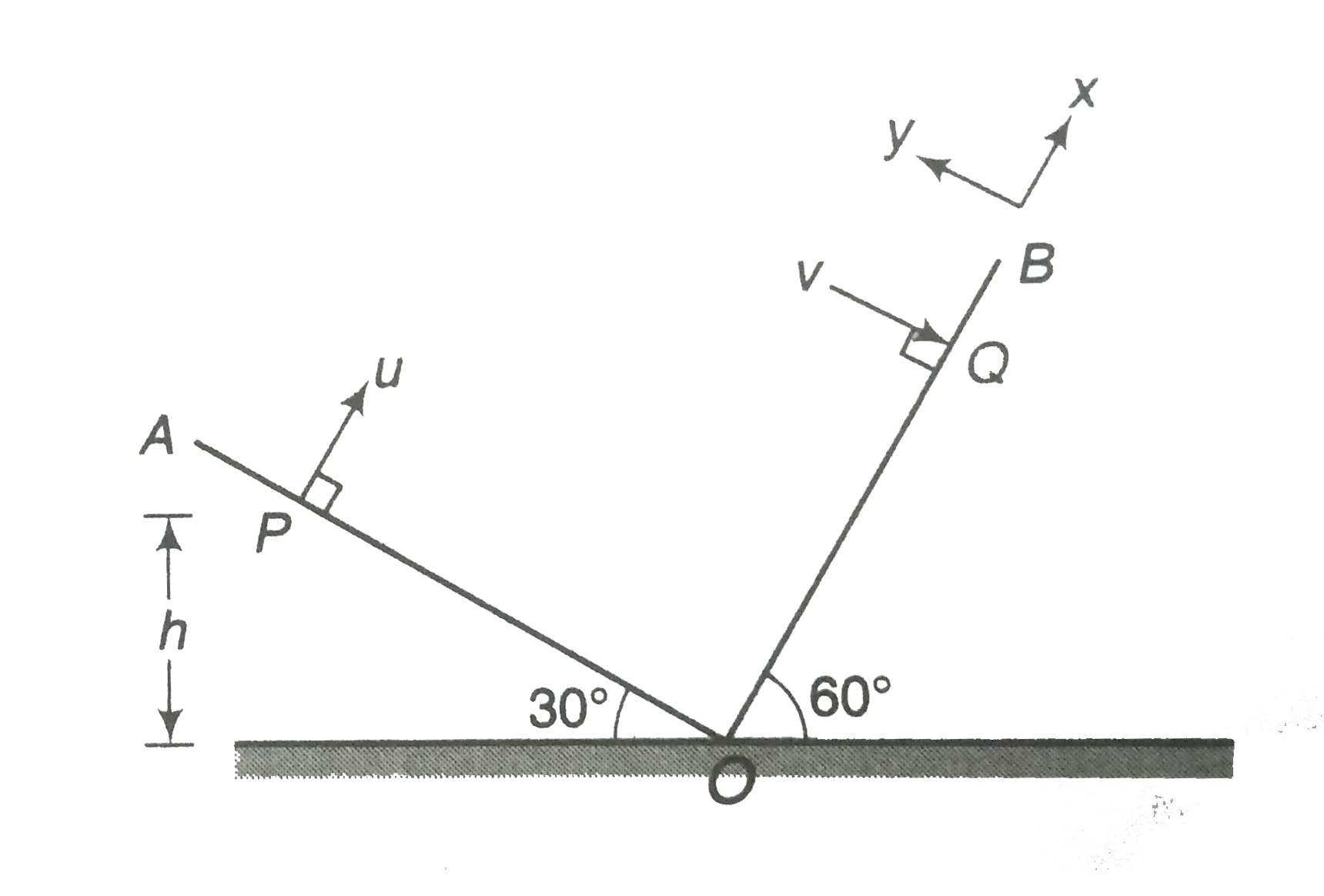
(a) time of flight,
(b) velocity with which the particle strikes the plane OB,
(c) height h of point P from point O,
(d) distance PQ. (Take g=10m/s2)
View SolutionTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.
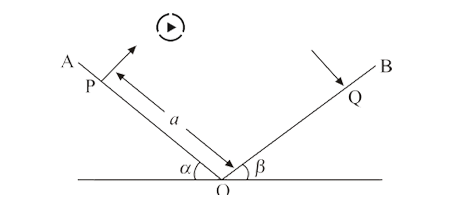
The path of the particle from P to Q is
View SolutionTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.

If α=30∘,β=30∘ the time of flight from P to Q is
View SolutionTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.

If α=30∘,β=30∘ the time of flight from P to Q is
View SolutionTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.
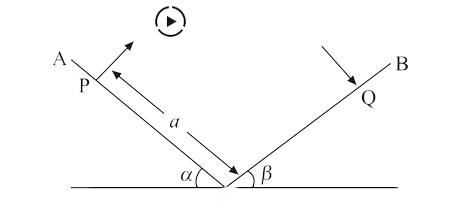
If α=30∘,β=30∘ and a = 4.9 m, the initial velocity of projection is
View SolutionTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.

If α=30∘,β=30∘ and a = 4.9 m, the initial velocity of projection is
View SolutionA ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is

View SolutionA particle is projected from the inclined plane at angle 37∘ with the inclined plane in upward direction with speed 10m/s. The angle of inclined plane with horizontal is 53∘. Then the maximum height attained by the particle from the inclined plane will be-
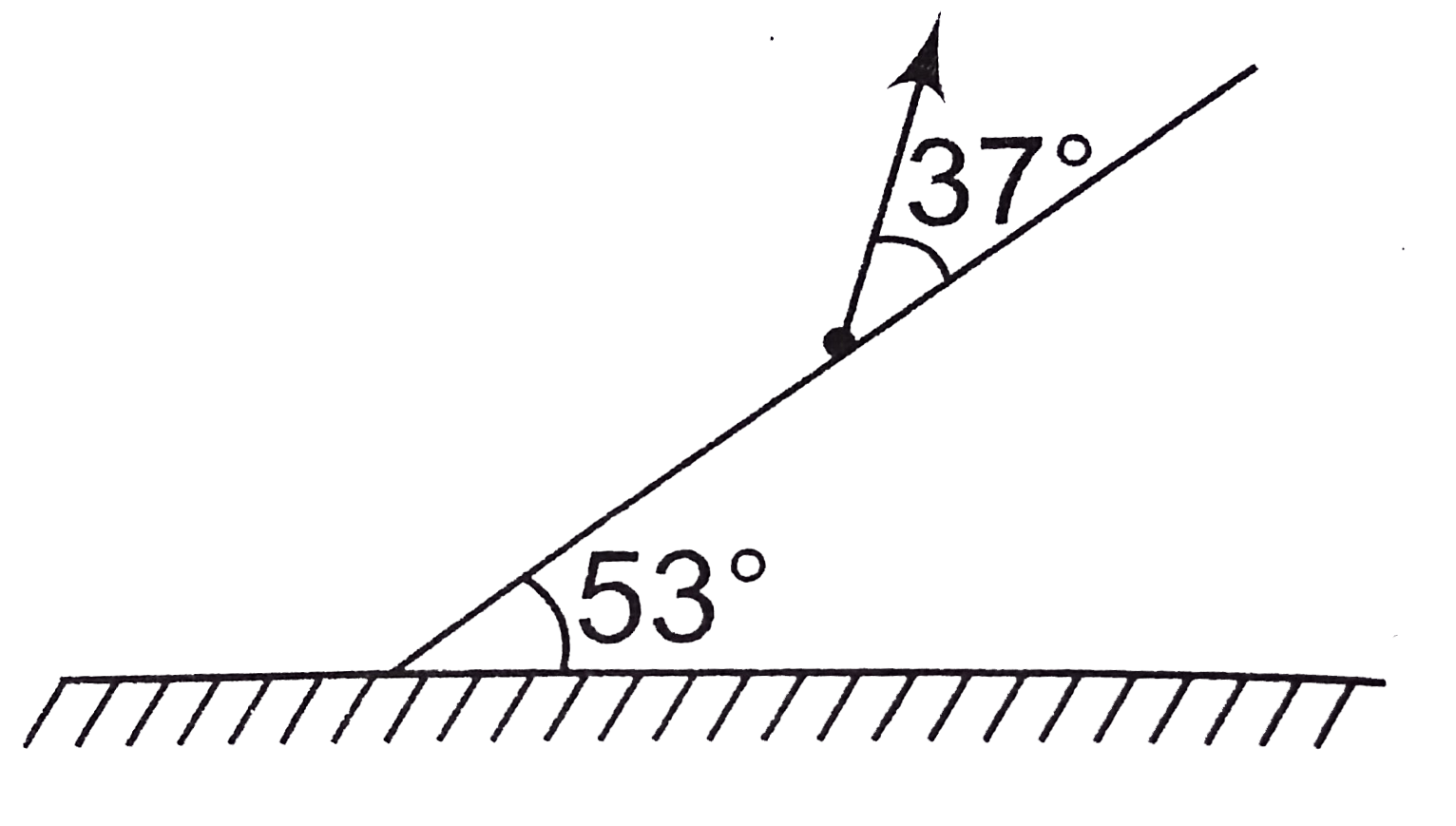
View Solution
