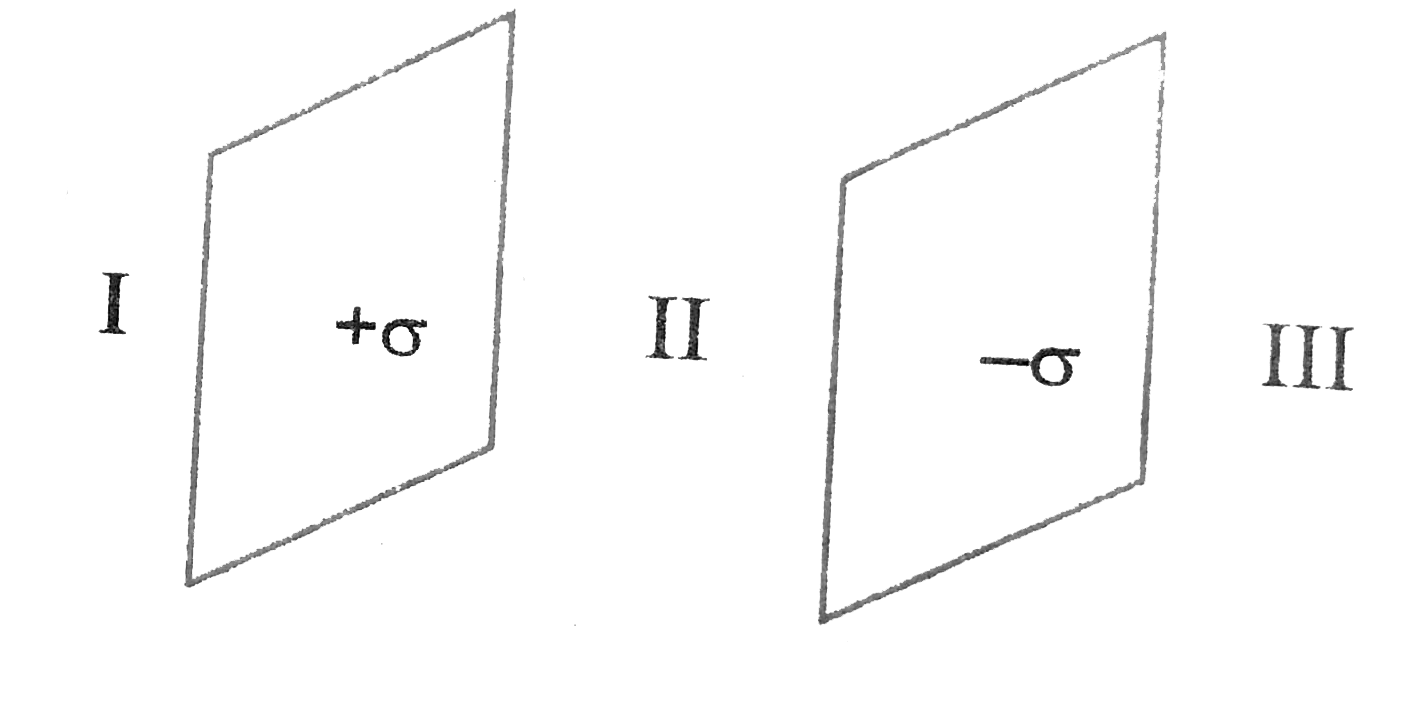
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 19×10−22Cm−2.
What is E (a) to the left of the plates (b) to the right of the plates (c) between the plates ?
Here, σ=19×10−22Cm−2
To solve the problem, we will calculate the electric field in three different regions: (a) to the left of the plates, (b) to the right of the plates, and (c) between the plates.
1. Understanding the Configuration:
- We have two parallel plates with surface charge densities of opposite signs. Let’s denote the surface charge density of the first plate as +σ and the second plate as −σ, where σ=19×10−22C/m2.
2. Electric Field Due to a Single Infinite Sheet:
- The electric field E due to a single infinite sheet of charge is given by the formula:
E=σ2ϵ0
- Here, ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
3. (a) Electric Field to the Left of the Plates:
- To the left of the plates, we consider a point where the electric fields from both plates will add up.
- The electric field due to the first plate (positive charge) points away from the plate, while the electric field due to the second plate (negative charge) also points away from it (towards the left).
- Therefore, the total electric field EA at this point is:
EA=E1+E2=σ2ϵ0+σ2ϵ0=σϵ0
- Substituting the value of σ:
EA=19×10−228.85×10−12≈2.14×10−10N/C
4. (b) Electric Field to the Right of the Plates:
- To the right of the plates, the electric fields from both plates will also add up.
- The electric field due to the first plate (positive charge) points away from it (to the right), and the electric field due to the second plate (negative charge) points towards it (also to the right).
- Therefore, the total electric field EB at this point is:
EB=E1+E2=σ2ϵ0+σ2ϵ0=σϵ0
- Thus, the electric field to the right of the plates is also:
EB=2.14×10−10N/C
5. (c) Electric Field Between the Plates:
- Between the plates, the electric field due to the first plate (positive charge) points away from it (to the right), and the electric field due to the second plate (negative charge) points towards it (to the left).
- Therefore, the total electric field EO at this point is:
EO=E1−E2=σ2ϵ0−(−σ2ϵ0)=σϵ0
- Substituting the value of σ:
EO=19×10−228.85×10−12≈2.14×10−10N/C
Final Results:
- (a) Electric field to the left of the plates: EA=2.14×10−10N/C
- (b) Electric field to the right of the plates: EB=2.14×10−10N/C
- (c) Electric field between the plates: EO=2.14×10−10N/C
- We have two parallel plates with surface charge densities of opposite signs. Let’s denote the surface charge density of the first plate as +σ and the second plate as −σ, where σ=19×10−22C/m2.
- The electric field E due to a single infinite sheet of charge is given by the formula:
E=σ2ϵ0
- Here, ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
- To the left of the plates, we consider a point where the electric fields from both plates will add up.
- The electric field due to the first plate (positive charge) points away from the plate, while the electric field due to the second plate (negative charge) also points away from it (towards the left).
- Therefore, the total electric field EA at this point is:
EA=E1+E2=σ2ϵ0+σ2ϵ0=σϵ0
- Substituting the value of σ:
EA=19×10−228.85×10−12≈2.14×10−10N/C
- To the right of the plates, the electric fields from both plates will also add up.
- The electric field due to the first plate (positive charge) points away from it (to the right), and the electric field due to the second plate (negative charge) points towards it (also to the right).
- Therefore, the total electric field EB at this point is:
EB=E1+E2=σ2ϵ0+σ2ϵ0=σϵ0
- Thus, the electric field to the right of the plates is also:
EB=2.14×10−10N/C
- Between the plates, the electric field due to the first plate (positive charge) points away from it (to the right), and the electric field due to the second plate (negative charge) points towards it (to the left).
- Therefore, the total electric field EO at this point is:
EO=E1−E2=σ2ϵ0−(−σ2ϵ0)=σϵ0
- Substituting the value of σ:
EO=19×10−228.85×10−12≈2.14×10−10N/C
- (a) Electric field to the left of the plates: EA=2.14×10−10N/C
- (b) Electric field to the right of the plates: EB=2.14×10−10N/C
- (c) Electric field between the plates: EO=2.14×10−10N/C
Similar Questions
Two large thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and magnitude 27×10−22Cm−2. The electric field →E in region II in between the plates is

View SolutionTwo large, thin metal plates are parallel and close to each other. On their faces, the plates have surfaces charge densities of opposite sign and of magnitude .177×10−11 coulomb per square metre. What is electric field
(i) to the left of the plates ?
(ii) to the right of the plates ?
(iii) in between the plates ?
View Solution
Knowledge Check
Two large, thin plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 16×10−22Cm−2. The electric field between the plates is
A1.8×10−10NC−1B1.9×10−10NC−1C1.6×10−10NC−1D1.5×10−10NC−1Two large parallel conducting plates are placed close to each other ,the inner surface of the two plates have surface charge densities +σ and −σ .The outer surfaces are without charge.The electric field has a magnitude of
Aσε0 in the region between the platesBσε0 in the region outside the plates.C2σε0 in the region between the platesDzero in the region outside the plates.Two large metal plates are placed parallel to each other The inner surfaces of plates are charge by +σand−σ(Cm−2) The outer surfaces are neutral .The electric field in the negion between the plates and outside the plates is
A2σε0,σε0Bσε0, zeroC2σε0, zeroDzero , 2σε0
Two large, thin metal plates are parallel and close to each other. On their faces, the plates have surfaces charge densities of opposite sign and of magnitude .177×10−11 coulomb per square metre. What is electric field
(i) to the left of the plates ?
(ii) to the right of the plates ?
(iii) in between the plates ?
View SolutionTwo large this metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and magnitude 17.0×10−22C/m2. What is →E : in the outer region of the first plate. (b) in the outer region of the secound plate, and (c) between the plates ? See Fig.
View SolutionTwo large, thin metal plates are parallel and close to each other , On their inner faces, the plates have surface charges densities of opposite signs and of magnitude 17.0×10−22C/m2.What is →E :
in the outer region of the first plate,
(b) in the outer region of the second plate,
(c) between the plates?
View SolutionTwo large conducting plates are placed parallel to each other nad they carry equal and opposite charges with surface density σ as shown in figure (30-E6). Find the electric field (a) at the left of the plates, (b) in between the plates and © at the right of the plates.

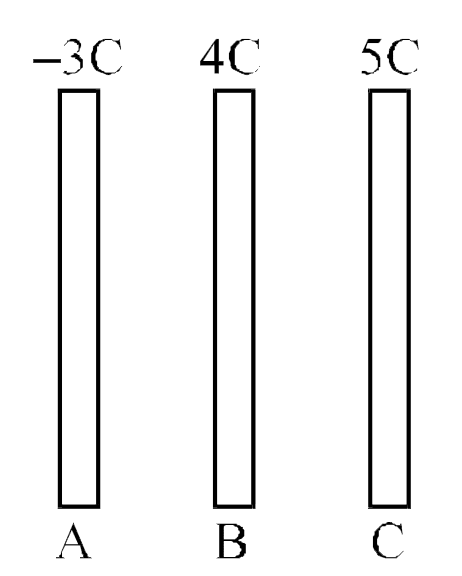
View SolutionThree large plates A, B and C are placed parallel to each other and charges are given as shown. The charge that appears on the left surface of plate B is
View Solution
