Two large vertical and parallel metal plates having a separation of 1cm are connected to a DC voltage source of potential difference X. A proton is released at rest midway between the two plates. It is found to move at 45∘ to the vertical JUST after release. Then X is nearly
1×10−5V
1×10−7V
1×10−9V
1×10−10V
To solve the problem step by step, we will analyze the motion of the proton in the electric field created by the two parallel plates.
Step 1: Understand the setup
We have two large vertical and parallel metal plates separated by a distance of 1 cm (0.01 m). These plates are connected to a DC voltage source, creating an electric field between them. A proton is released at rest midway between the plates.
Step 2: Identify the forces acting on the proton
When the proton is released, it experiences two forces:
1. The gravitational force acting downward, Fg=mg, where m is the mass of the proton and g is the acceleration due to gravity.
2. The electric force acting upward due to the electric field E, given by Fe=qE, where q is the charge of the proton.
Step 3: Determine the angle of motion
It is given that the proton moves at a 45∘ angle to the vertical just after release. This implies that the magnitudes of the forces acting on the proton are equal:
Fg=Fe
Thus, we can write:
mg=qE
Step 4: Relate electric field to voltage
The electric field E between two parallel plates is given by:
E=Vd
where V is the potential difference (voltage) across the plates and d is the separation between the plates.
Step 5: Substitute E in the force equation
Substituting the expression for E into the force equation gives:
mg=q(Vd)
Step 6: Rearranging the equation to find V
Rearranging the equation to solve for V yields:
V=mgdq
Step 7: Substitute known values
Now we can substitute the known values:
- Mass of proton, m=1.67×10−27 kg
- Acceleration due to gravity, g=9.8 m/s²
- Separation between plates, d=0.01 m
- Charge of proton, q=1.6×10−19 C
Substituting these values into the equation:
V=(1.67×10−27kg)⋅(9.8m/s2)⋅(0.01m)1.6×10−19C
Step 8: Calculate V
Calculating the numerator:
1.67×10−27⋅9.8⋅0.01=1.63×10−28kg m/s2
Now, dividing by the charge of the proton:
V=1.63×10−281.6×10−19=1.02×10−9V
Step 9: Final answer
Thus, the potential difference X is nearly:
X≈1×10−9V
We have two large vertical and parallel metal plates separated by a distance of 1 cm (0.01 m). These plates are connected to a DC voltage source, creating an electric field between them. A proton is released at rest midway between the plates.
When the proton is released, it experiences two forces:
1. The gravitational force acting downward, Fg=mg, where m is the mass of the proton and g is the acceleration due to gravity.
2. The electric force acting upward due to the electric field E, given by Fe=qE, where q is the charge of the proton.
It is given that the proton moves at a 45∘ angle to the vertical just after release. This implies that the magnitudes of the forces acting on the proton are equal:
Fg=Fe
Thus, we can write:
mg=qE
The electric field E between two parallel plates is given by:
E=Vd
where V is the potential difference (voltage) across the plates and d is the separation between the plates.
Substituting the expression for E into the force equation gives:
mg=q(Vd)
Rearranging the equation to solve for V yields:
V=mgdq
Now we can substitute the known values:
- Mass of proton, m=1.67×10−27 kg
- Acceleration due to gravity, g=9.8 m/s²
- Separation between plates, d=0.01 m
- Charge of proton, q=1.6×10−19 C
V=(1.67×10−27kg)⋅(9.8m/s2)⋅(0.01m)1.6×10−19C
Calculating the numerator:
1.67×10−27⋅9.8⋅0.01=1.63×10−28kg m/s2
Now, dividing by the charge of the proton:
V=1.63×10−281.6×10−19=1.02×10−9V
Thus, the potential difference X is nearly:
X≈1×10−9V
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
A parallel plate air-core capacitor is connected across a source of constant potential difference. When a dielectric plate is introduced between the two plates then:
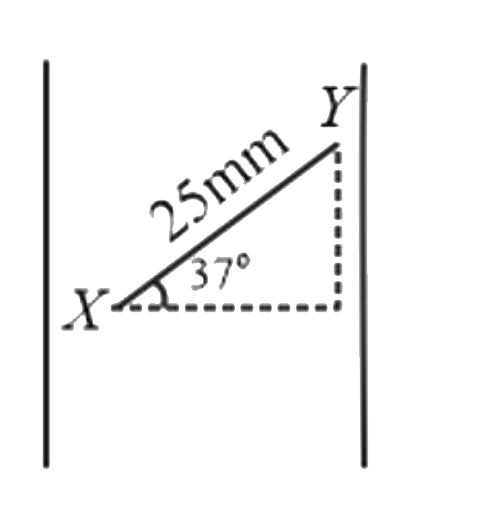
View SolutionTwo large parallel conducting plates are separated by 40 mm. The potential difference between the plates is V. Potential difference between points X and Y as indicated in the figure will be
View SolutionTwo square plates are at potential difference of 100V separated by 2cm. Calculate electric intensity between them
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
_2019_CBT2_E01_002_Q01.png)
View SolutionTwo parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionAn electric field of magnitude 1000NC−1 is produced between two parallel platees having a separation of 2.0 cm as shown in figure(29.E4) (a) What is the potential difference between the plates? (b) With what minimum speed should an electron be projected from the lower plate in the direction of the field so that it may reach the upper plate? ( c) Suupose the electron is projected from the lower plate with the speed calculated in part (b) . The direction of projection makes an angle of 60∘ with the field. Find the mazimum height reached by the electron.

View SolutionTwo protons A and B are placed in between the two plates of a parallel plate capacitor charged to a potential difference V as shown in the figure. The forces on the two protons are identical.

View SolutionTwo parallel plate capacitors are filled with dielectrics and connected separately across same potential difference as shown in figure. Their plate area is A and separation between plates is 'd'. Then the ration of energy stored is:
_2019_CBT7_E01_016_Q01.png)
View SolutionThe plates of a parallel plate capacitor are charged to a potential difference of 117 V and then connected across a resistor. The potential difference across the capacitor decreases exponentially with to time.After 1s the potential difference between the plates is 39 V, then after 2s from the start, the potential difference (in V) between the plates is
View SolutionTwo parallel plate capacitors are filled with dielectrics and connected speparately across same potential difference as shown in figure. Their plate area is A and separation between plates is 'd'. Then the ration of energy stored is:
_2019_CBT7_E01_016_Q01.png)
View Solution
