Two monochromatic (wavelength = a/5) and coherent sources of electromagnetic waves are placed on the x-axis at the points (2a,0) and (-a,0). A detector moves in a circle of radius R(gtgt2a) whose centre is at the origin. The number of maxima detected during one circular revolution by the detector are
60
15
64
None of these
The correct Answer is:A
To solve the problem, we need to determine the number of maxima detected by a detector moving in a circular path around two coherent sources of electromagnetic waves. The sources are located at (2a, 0) and (-a, 0) on the x-axis, and the wavelength of the waves is given as λ = a/5.
1. Identify the positions of the sources:
- The first source (S1) is at (2a, 0).
- The second source (S2) is at (-a, 0).
2. Calculate the distance between the two sources:
Δx=2a−(−a)=2a+a=3a
3. Determine the wavelength:
- Given that the wavelength λ=a5.
4. Calculate the number of wavelengths in the distance between the sources:
Number of wavelengths=Δxλ=3aa5=3a⋅5a=15
This means that the distance between the two sources corresponds to 15 wavelengths.
5. Understanding the maxima formation:
- Maxima occur when the path difference between the two waves from the sources to the detector is an integer multiple of the wavelength.
- The path difference can range from 0 to 15λ.
6. Counting the maxima:
- The path difference can take values: 0,λ,2λ,…,15λ.
- This gives us a total of 15+1=16 possible values (including 0).
7. Considering the circular motion of the detector:
- As the detector moves in a circle, it will encounter maxima at various angles corresponding to the path differences.
- The maxima will occur at the points where the path difference is nλ for n=0,1,2,…,15.
8. Final count of maxima:
- Since there are 15 intervals between the maxima (from 0 to 15) and each interval can be counted at two points (one on either side of the midpoint), we multiply the number of intervals by 4 (for each quadrant).
- Therefore, the total number of maxima is:
15 intervals×4=60
Conclusion:
The total number of maxima detected during one circular revolution by the detector is 60.
- The first source (S1) is at (2a, 0).
- The second source (S2) is at (-a, 0).
Δx=2a−(−a)=2a+a=3a
- Given that the wavelength λ=a5.
Number of wavelengths=Δxλ=3aa5=3a⋅5a=15
This means that the distance between the two sources corresponds to 15 wavelengths.
- Maxima occur when the path difference between the two waves from the sources to the detector is an integer multiple of the wavelength.
- The path difference can range from 0 to 15λ.
- The path difference can take values: 0,λ,2λ,…,15λ.
- This gives us a total of 15+1=16 possible values (including 0).
- As the detector moves in a circle, it will encounter maxima at various angles corresponding to the path differences.
- The maxima will occur at the points where the path difference is nλ for n=0,1,2,…,15.
- Since there are 15 intervals between the maxima (from 0 to 15) and each interval can be counted at two points (one on either side of the midpoint), we multiply the number of intervals by 4 (for each quadrant).
- Therefore, the total number of maxima is:
15 intervals×4=60
The total number of maxima detected during one circular revolution by the detector is 60.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 More Than One Correct
6 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Comprehensionn Based
4 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Single Correct
11 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
Four monochromatic and coherent sources of light, emitting waves in phase of wavelength λ, are placed at the points x = 0, d 2d and 3d on the x-axis. Then
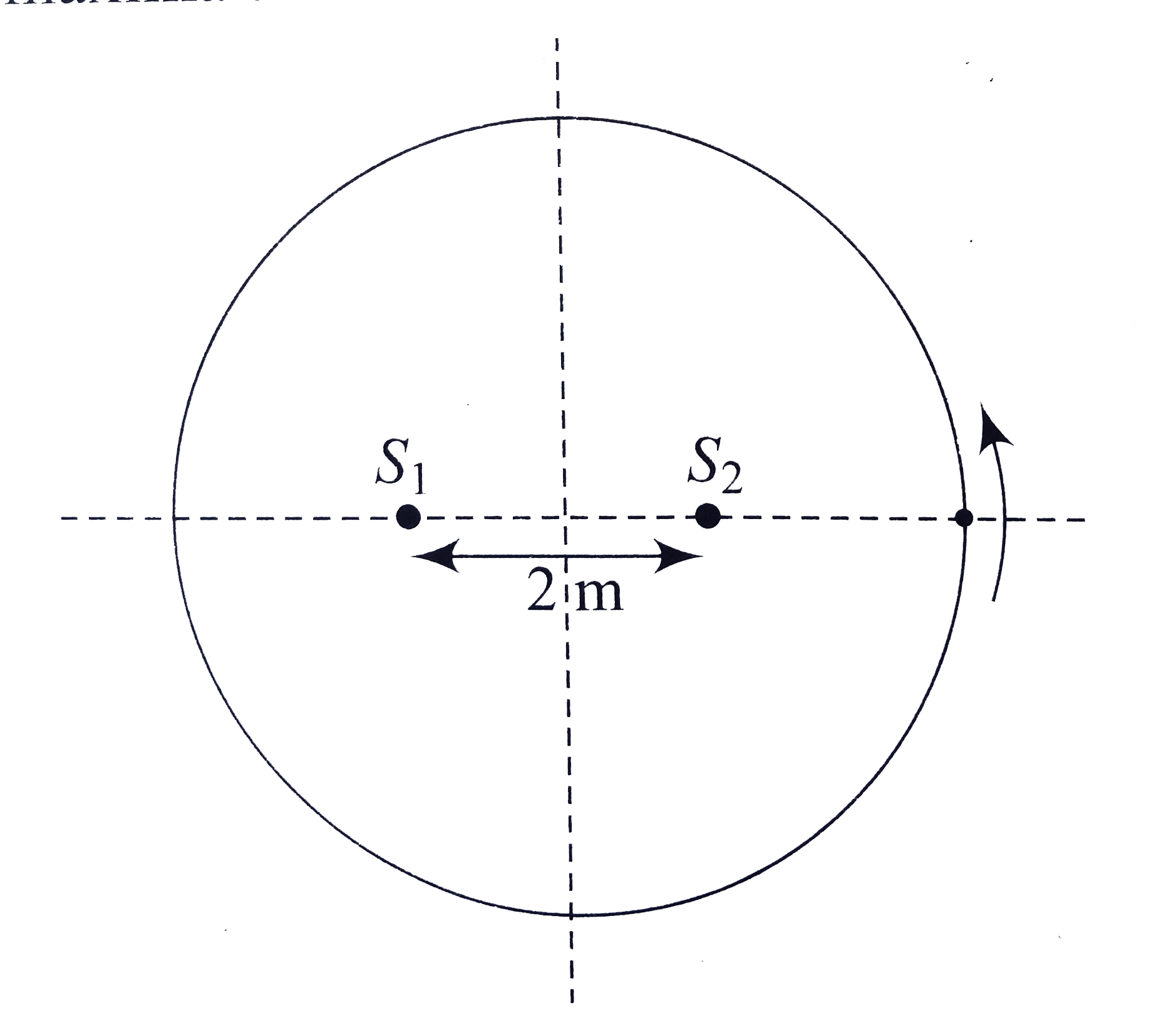
View SolutionTwo point sources separated by 2.0 m are radiating in phase with λ=0.50m. A detector moves in a circular path around the two sources in a plane containing them. How many maxima are detected?
View SolutionIf the point (x,4) lies on a circle whose centre is at the origin and radius is 5, then x= ±5 (b) ±3 (c) 0 (d) 14
View SolutionFind the equation of a circle of radius 5 units whose centre lies on x-axis and passes through the point (2, 3).
View SolutionFind the equation of a circle of radius 5 whose centre lies on x-axis and passes through the point (2,3).
View SolutionFind the equation of the circle with radius 5 whose center lies on the x-axis and passes through the point (2, 3).
View SolutionTwo coherent sources separated by distance d are radiating in phase having wavelength λ. A detector moves in a big circle around the two sources in the plane of the two sources. The angular position of n=4 interference maxima is given as

View SolutionIf a circle of radius 4 touches x-axis at (2,0) then its centre may be
View SolutionThe line 2x - y + 1 = 0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x-2y = 4. The radius of the circle is :
View SolutionFour monochromatic and coherent sources of light emitting waves in phase at placed on y axis at y = 0, a, 2a and 3a. If the intensity of wave reaching at point P far away on y axis from each of the source is almost the same and equal to I0, then the resultant intensity at P for a=λ8 is nI0. The value of [n] is.
Here [] is greatest integer funciton.
View Solution
