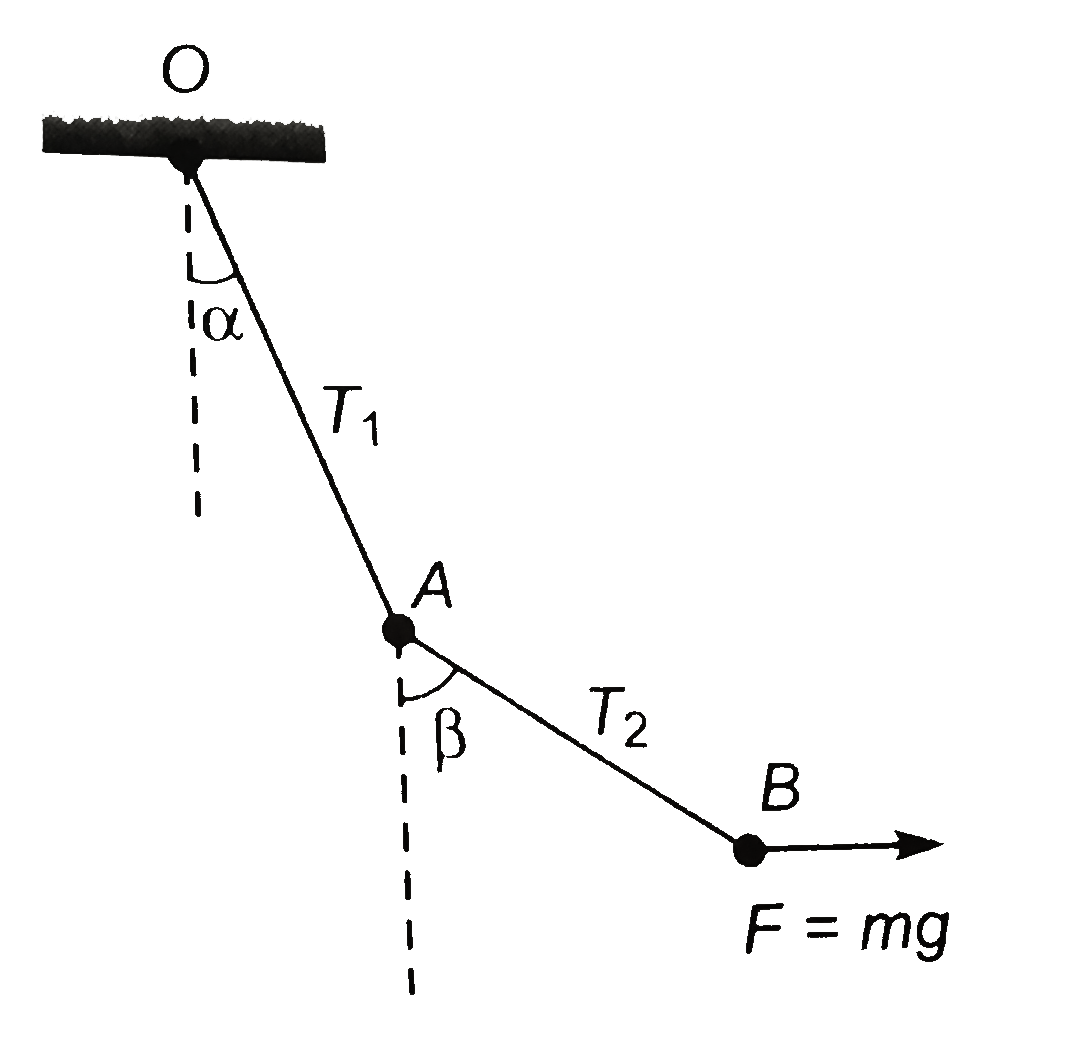
Two particalA and B each of mass m are kept stationary by applying a horizontal force F=mg on partical B as show in figure .Then
tanβ=2tanα
2T1=5T2
√2T1=√5T2
α=β
The correct Answer is:A, C
Resultant of mg and mg is √2mg.
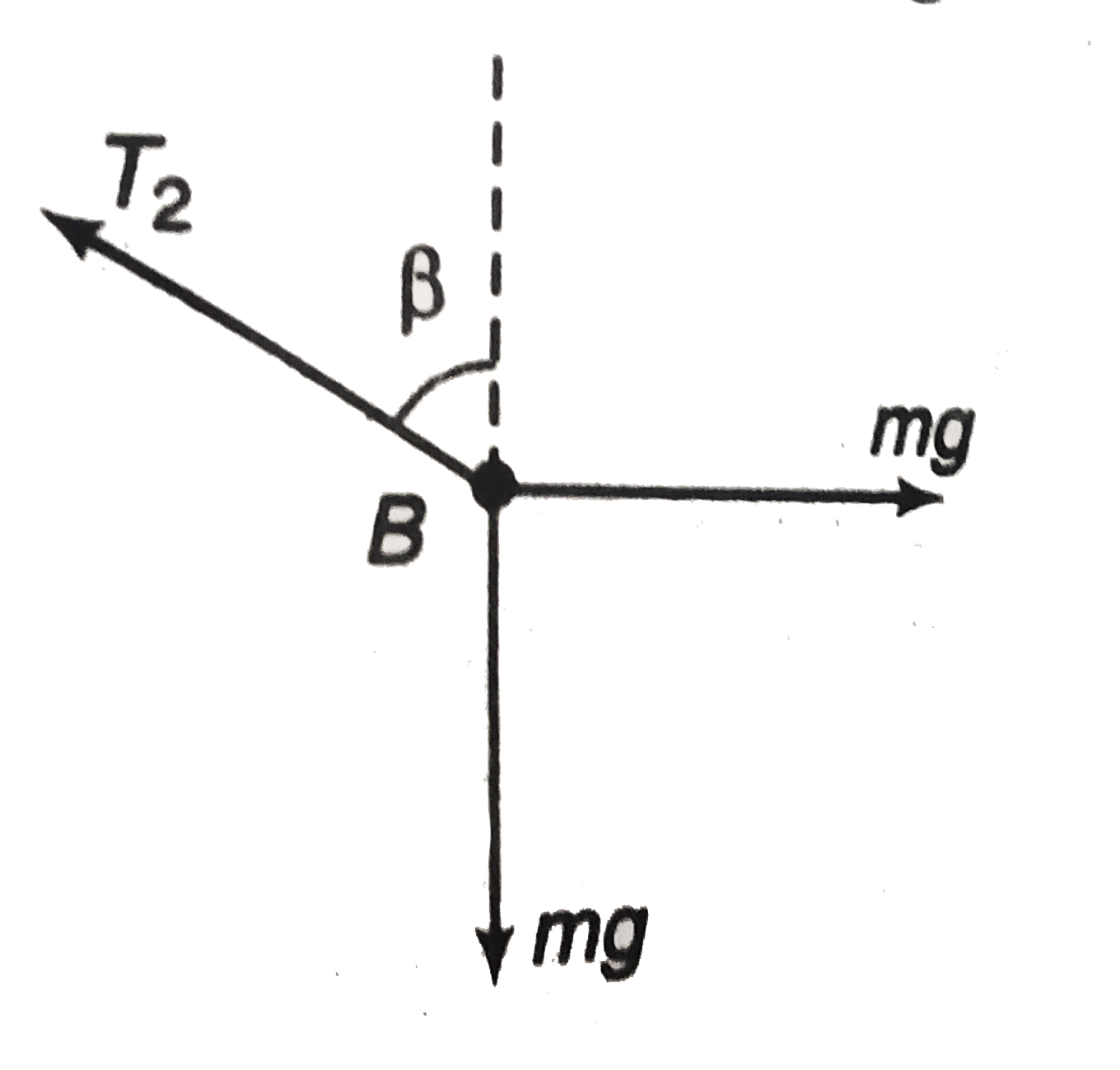
Therefore T2 should be equal and opposite of this .
or T2=√2mg…(i)
Further, T2cosβ=mg …(ii)
and T2cosβ=mg …(iii)
or sinβ=cosβ⇒β=45∘
T1cosα=mg+T2cosβ
=mg+√2mg(1√2)
or T1cosα=2mg ...(iv)
T1sinα=T2sinβ=√2mg(1√2)
T1sinα=mg ...(v)
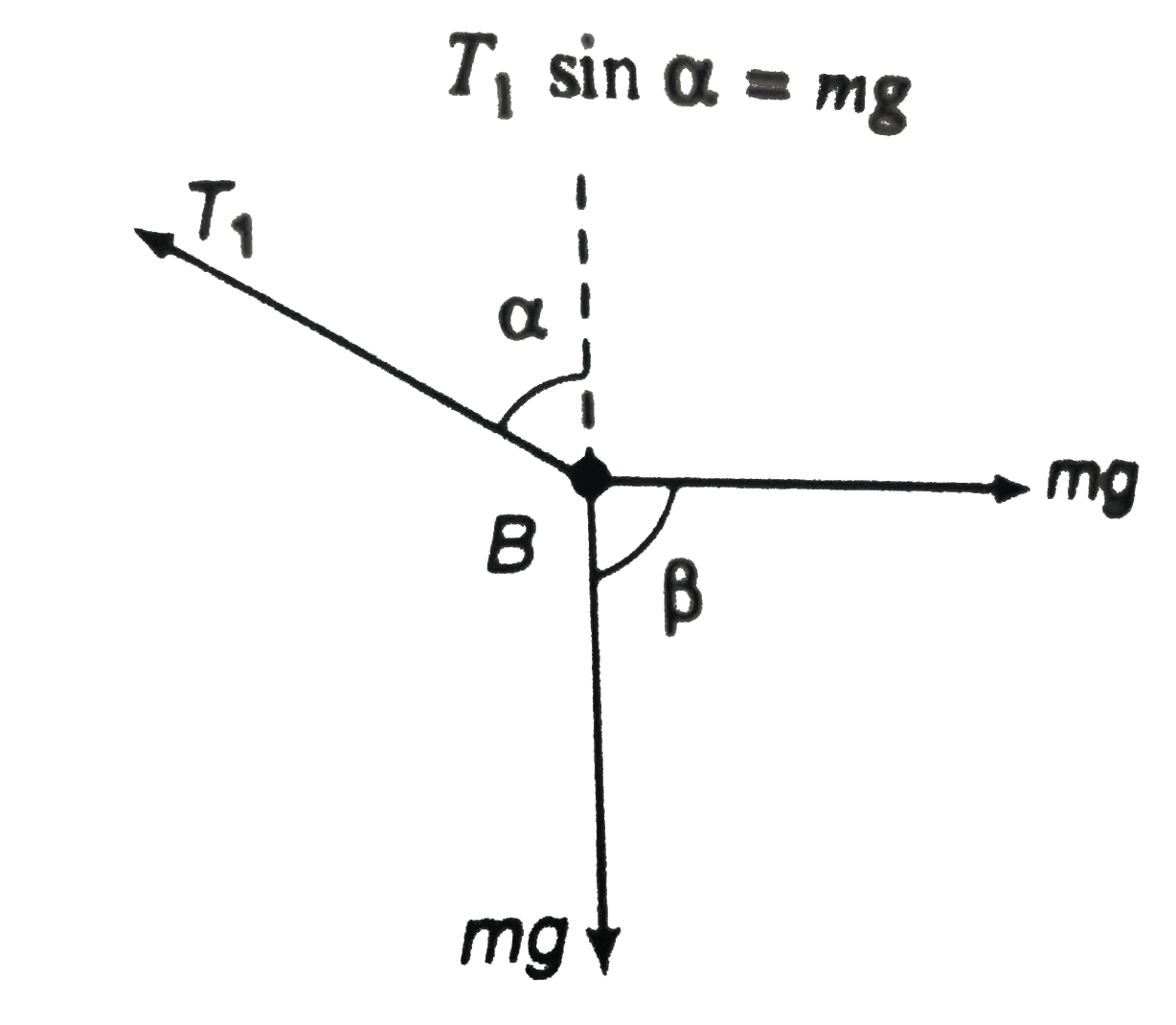
From Eqs. (iv) and (v), we get
tanα=12 and T1=√5mg
tanβ=tan45∘=1 and T2=√2mg
∴tanβ=2tanα and √2T1=√5T2
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Subjective Question
27 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Single Correct
90 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
Two masses A and B, each of mass M are fixed together by a massless spring. A force acts on the mass B as shown in figure. If the mass A starts moving away from mass B with acceleration 'a', then the acceleration of mass B wil be :-

View SolutionTwo blocks A and B of masses 2kg and 4kg are placed one over the other as shown in figure. Atime varying horizontal force F=2t is applied on the upper block as shown in figure. Here t is in second and F is in newton. Drow a graph showing acceleration of A and B on y-axis and time on x-axis.Coefficient of friction between A and B is μ=12 and the horizontal surface over which B is placed smooth. (g=10m/s2)

View Solution
Knowledge Check
Two particles A and B each of mass m are kept stationary by applying a horizontal force F=mg on particle B as show in figure .Then
 A2tanβ=tanαB2T1=5T2CT1√2=T2√5DNone of these
A2tanβ=tanαB2T1=5T2CT1√2=T2√5DNone of theseTwo particle A & B each of mass m are in equilibrium in a vertical plane under action of a horizontal force F=mg on particle B, as shown in figure Then :
 A2T1=5T2BT1√2=T2√5Ctanθ=2tanαDNone of these
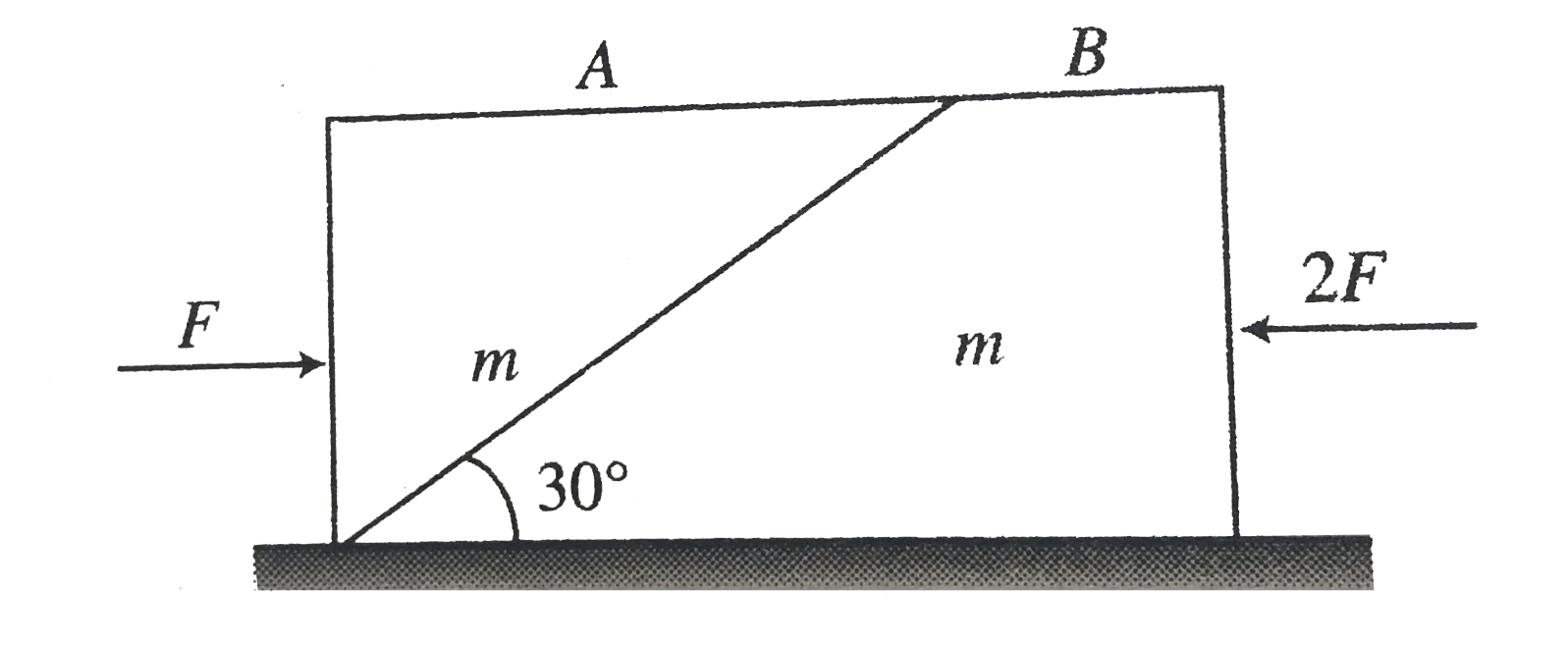
A2T1=5T2BT1√2=T2√5Ctanθ=2tanαDNone of theseTwo blocks A and B each of mass m are placed on a smooth horizontal surface. Two horizontal force F and 2F are applied on blocks A and B, respectively, as shown in fig. Block A does not slide on block B. Then then the normal reaction acting between the two blocks is (assume no friction between the blocks)
 AFBF/2CF√3D3F
AFBF/2CF√3D3F
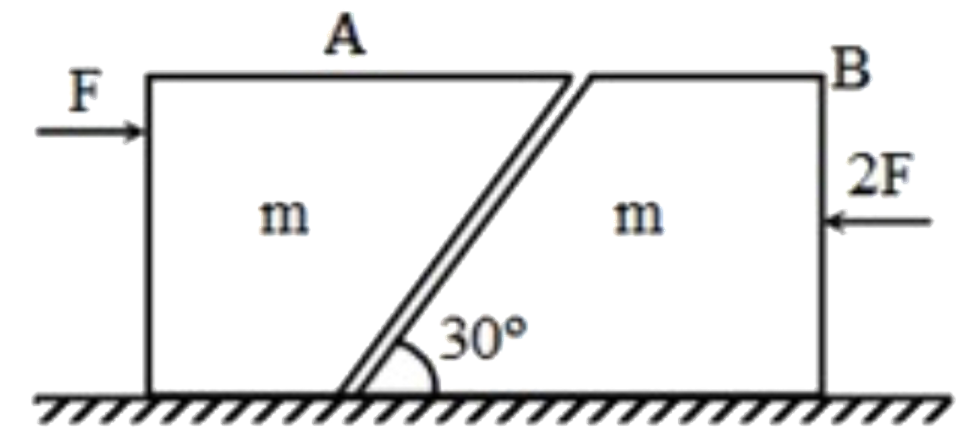
Two blocks 'A' and 'B' each of mass 'm' are placed on a smooth horizontal surface . Two horizontal force F and 2F are applied on the blocks A and B , respectively , as shown in figure . The block A does not slide on block B . The normal reaction acting between the two blocks is
View SolutionA block of mass'm' it kept over the smooth surface of the plank of mass M. the plank of length l is kept over the smooth horizontal surface. A constant horizontal force F is applied onto the plank as shown in figure. Calculate the time after which the block falls off the plank?

View SolutionTwo identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. If the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
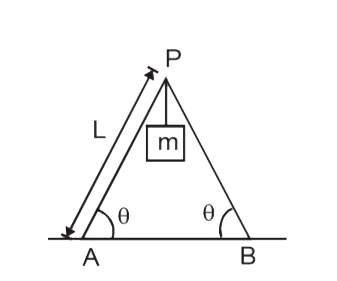
View SolutionTwo identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. if the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
View SolutionFour blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.

View Solution
