Two particles connected by a rigid light rod AB, lying on a smooth horizontal table. An impulse J is applied at A in the plane of thetable and perpendicular at AB. Then the velocity of particle at A is
J2m
Jm
2Jm
zero
The correct Answer is:B
To solve the problem, we need to analyze the motion of the two particles connected by a rigid light rod when an impulse J is applied at point A. The steps to find the velocity of particle A are as follows:
1. Understanding the System:
- We have two particles connected by a rigid light rod AB on a smooth horizontal table.
- An impulse J is applied at point A perpendicular to the rod.
2. Impulse and Change in Momentum:
- The impulse J causes a change in momentum. Since the initial momentum is zero, the change in momentum is equal to the impulse:
Δp=J
3. Velocity of the Center of Mass (CM):
- The total mass of the system is 2m (assuming each particle has mass m).
- The velocity of the center of mass VCM can be calculated using the formula:
VCM=ΔpTotal mass=J2m
4. Angular Motion:
- The impulse also causes the rod to rotate about the center of mass. We need to find the angular velocity ω of the rod.
- The angular impulse is given by:
Angular Impulse=J⋅L2
where L is the length of the rod.
5. Moment of Inertia:
- The moment of inertia I of the system about the center of mass is:
I=m(L2)2+m(L2)2=mL24+mL24=mL22
6. Relating Angular Impulse to Angular Momentum:
- The angular impulse is equal to the change in angular momentum:
J⋅L2=I⋅ω
- Substituting for I:
J⋅L2=mL22⋅ω
- Solving for ω:
ω=JmL
7. Velocity of Point A:
- The total velocity of point A is the sum of the translational velocity of the center of mass and the rotational velocity due to angular motion:
VA=VCM+ω⋅L2
- Substituting the values:
VA=J2m+(JmL)⋅L2
- Simplifying:
VA=J2m+J2m=Jm
Final Answer:
The velocity of particle A is:
VA=Jm
- We have two particles connected by a rigid light rod AB on a smooth horizontal table.
- An impulse J is applied at point A perpendicular to the rod.
- The impulse J causes a change in momentum. Since the initial momentum is zero, the change in momentum is equal to the impulse:
Δp=J
- The total mass of the system is 2m (assuming each particle has mass m).
- The velocity of the center of mass VCM can be calculated using the formula:
VCM=ΔpTotal mass=J2m
- The impulse also causes the rod to rotate about the center of mass. We need to find the angular velocity ω of the rod.
- The angular impulse is given by:
Angular Impulse=J⋅L2
where L is the length of the rod.
- The moment of inertia I of the system about the center of mass is:
I=m(L2)2+m(L2)2=mL24+mL24=mL22
- The angular impulse is equal to the change in angular momentum:
J⋅L2=I⋅ω
- Substituting for I:
J⋅L2=mL22⋅ω
- Solving for ω:
ω=JmL
- The total velocity of point A is the sum of the translational velocity of the center of mass and the rotational velocity due to angular motion:
VA=VCM+ω⋅L2
- Substituting the values:
VA=J2m+(JmL)⋅L2
- Simplifying:
VA=J2m+J2m=Jm
The velocity of particle A is:
VA=Jm
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance l6 from the centre towards A of the rod after time t=πml12J is.
View SolutionTwo particles each of mass M are connected by a massless rod. The rod is lying on the smooth horizontal surface. If one of the particle is given an impulse MV as shown in the figure then angular velocity of the system would be:

View SolutionTwo bodies of masses 4 kg and 6 kg connected by means of a light string are lying on a smooth horizontal surface. A horizontal pulling force is applied on the lighter body. Two seconds later the string connecting the two masses is cut. After two more seconds if the velocity of the heavier mass is 2ms−1, the force initially applied is
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionTwo particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
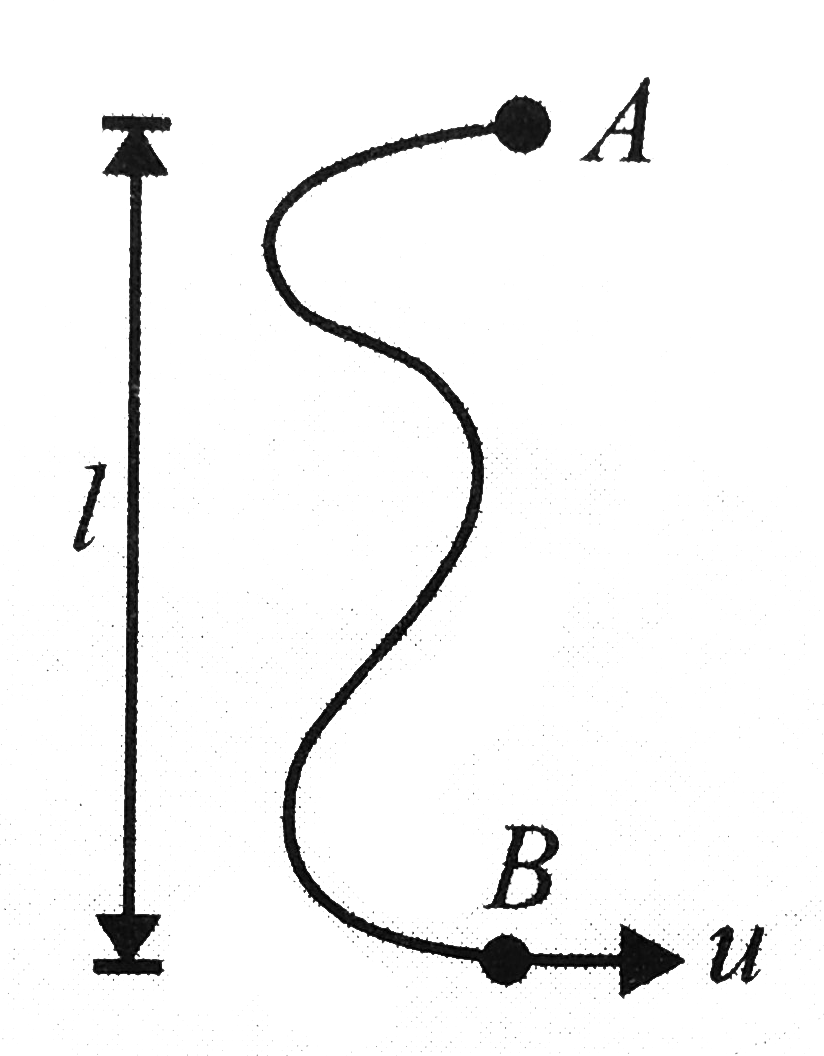
View SolutionTwo particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the position shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
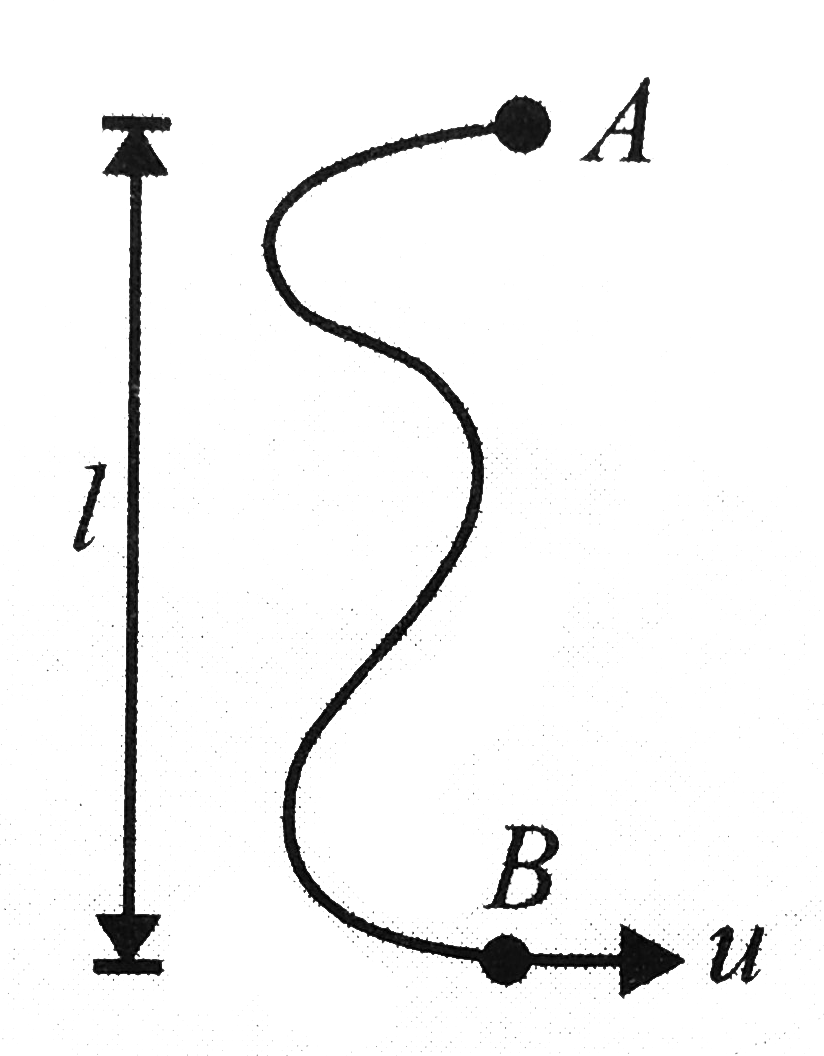
View SolutionTwo masses A and B connected with an inextensible string of length l lie on a smooth horizontal plane. A is given a velocity of vm/s along the ground perpendicular to line AB as shown in figure. Find the tension in string during their subsequent motion

View SolutionThe adjacent figure shows a non-uniform metre stick AB having the linear mass density variation λ=λ0x , where λ0 is a constant and x is the distance from end A, placed on a smooth horizontal surface. In the first experiment, the rod is pivoted at A and force F is applied perpendicular to the rod at the other end B and in the second experiment, the rod is pivoted at B and the force is applied perpendicular to the rod at the end A. If in the first case angular acceleration is αA and in the second case it is αB then
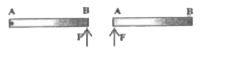
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View Solution
