Two particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time

The correct Answer is:(a) T=2pi sqrt((m_(1)m_(2))/((m_(1)+m_(2))k))<br> (b) (m_(2)L)/(m_(1)+m_(2))=A_(1)<br>(c ) X_(1)=V_(0^(t))-A_(1)(1-cos omegat);<br>X_(2)=V_(0^(t))-A_(2)(1-cos omegat)
Where
A1=m2Lm1+m2;A2=m1Lm1m2;ω=√k(m1+m2)m1m2
Topper's Solved these Questions
Similar Questions
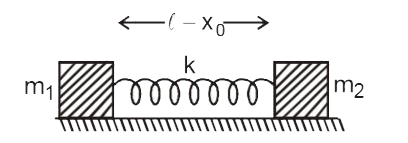
Two blocks of mass m1 and m2 are connected with a spring of natural length l and spring constant k. The system is lying on a smooth horizontal surface. Initially spring is compressed by x0 as shown in figure. Show that the two blocks will perform SHM about their equilibrium position. Also (a) find the time period, (b) find amplitude of each block and (c) length of spring as a function of time.
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View Solution
Knowledge Check
A ball of mass 1kg moving with velocity 3m/s, collides with spring of natural length 2m and force constant 144N/m . What will be length of compressed spring ?
A2mB1.5mC1mD0.5mA ball of mass 2 kg moving with velocity 3m/s collides with spring of natural length 2 m and force constant 144N/m What will be length of compressed spring ?
A2 mB1.5 mC1 mD0.5 mA ball of mass 2 kg moving with velocity 3m/s collides with spring of natural length 2 m and force constant 144N/m What will be length of compressed spring ?
A2 mB1.5 mC1 mD0.5 m
Two blocks of masses m1andm2 are connected by a spring of spring constant k figure. The block of mass m2 is given a shape impulse so that it acquires a velocity v0 towards right. Find a. the velocity of the centre of mass b. the maximum elongation that the spring will suffer.
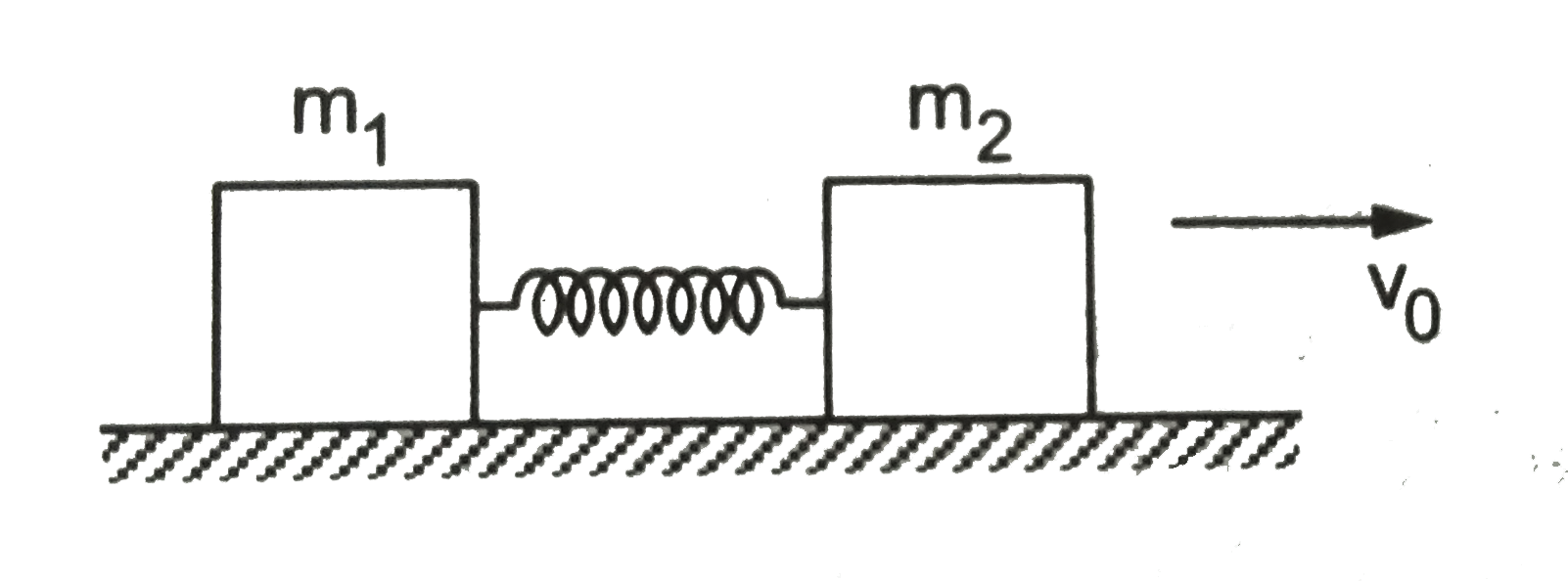
View SolutionTwo blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

View SolutionTwo blocks are connected by a spring of natural length 2 m. The force constant of spring is 200 N/m.
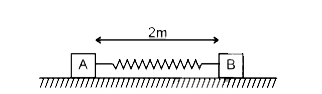
Find spring force in following situations :
A is kept at rest and B is displaced by 1 m in right direction.
View SolutionTwo blocks are connected by a spring of natural length 2 m. The force constant of spring is 200 N/m.

Find spring force in following situations :
B is kept at rest and A is displaced by 1m in left direction.
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View Solution
