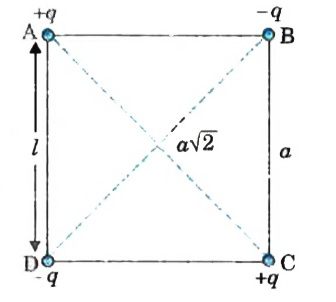
Two point charges +Q each are placed at adjacent corners of a square. Other two point charges -Q each are placed at the remaining two corners of the same square . The side of the square is l. Find electric field intensity at the centre of the square.
To find the electric field intensity at the center of the square with the given charges, we can follow these steps:
Step 1: Understand the Configuration
We have a square with side length l. At two adjacent corners, we have positive charges +Q, and at the other two corners, we have negative charges −Q.
Step 2: Determine the Position of the Center
The center of the square is located at equal distances from all four corners. The distance from each corner to the center can be calculated using the Pythagorean theorem. The distance a from a corner to the center is given by:
a=l√2
Step 3: Calculate the Electric Field Due to Each Charge
The electric field E due to a point charge is given by:
E=k|Q|r2
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge to the point where the field is being calculated.
For our case, the electric field at the center due to each charge +Q is:
E+=kQ(l√2)2=2kQl2
And the electric field due to each charge −Q is:
E−=kQ(l√2)2=2kQl2
Step 4: Determine the Direction of the Electric Fields
- The electric field due to the positive charges +Q will point away from the charges.
- The electric field due to the negative charges −Q will point towards the charges.
Step 5: Resolve the Electric Fields into Components
Since the positive charges are at adjacent corners, their electric fields will have components that can be resolved into x and y directions. The same applies to the negative charges.
- For the two positive charges:
- The x-component of the electric field from each +Q charge is E+x=E+cos(45∘)=E+√2
- The y-component is the same: E+y=E+sin(45∘)=E+√2
- For the two negative charges:
- The x-component of the electric field from each −Q charge is E−x=E−cos(45∘)=E−√2 (pointing towards the charge)
- The y-component is the same: E−y=E−sin(45∘)=E−√2
Step 6: Calculate the Net Electric Field Components
- The total electric field in the x-direction:
Enet,x=2E+x−2E−x=2(E+√2)−2(E−√2)=2(E+−E−√2)
- The total electric field in the y-direction:
Enet,y=2E+y−2E−y=2(E+√2)−2(E−√2)=2(E+−E−√2)
Step 7: Calculate the Magnitude of the Net Electric Field
The magnitude of the net electric field Enet can be found using:
Enet=√E2net,x+E2net,y
Since Enet,x=Enet,y, we can simplify this to:
Enet=√2Enet,x
Step 8: Substitute the Values
Substituting E+ and E− into the equations gives us the final expression for the electric field intensity at the center of the square.
Final Expression
The final expression for the electric field intensity at the center of the square is:
Enet=4kQl2
We have a square with side length l. At two adjacent corners, we have positive charges +Q, and at the other two corners, we have negative charges −Q.
The center of the square is located at equal distances from all four corners. The distance from each corner to the center can be calculated using the Pythagorean theorem. The distance a from a corner to the center is given by:
a=l√2
The electric field E due to a point charge is given by:
E=k|Q|r2
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge to the point where the field is being calculated.
E+=kQ(l√2)2=2kQl2
And the electric field due to each charge −Q is:
E−=kQ(l√2)2=2kQl2
- The electric field due to the positive charges +Q will point away from the charges.
- The electric field due to the negative charges −Q will point towards the charges.
Since the positive charges are at adjacent corners, their electric fields will have components that can be resolved into x and y directions. The same applies to the negative charges.
- The x-component of the electric field from each +Q charge is E+x=E+cos(45∘)=E+√2
- The y-component is the same: E+y=E+sin(45∘)=E+√2
- The x-component of the electric field from each −Q charge is E−x=E−cos(45∘)=E−√2 (pointing towards the charge)
- The y-component is the same: E−y=E−sin(45∘)=E−√2
- The total electric field in the x-direction:
Enet,x=2E+x−2E−x=2(E+√2)−2(E−√2)=2(E+−E−√2)
Enet,y=2E+y−2E−y=2(E+√2)−2(E−√2)=2(E+−E−√2)
The magnitude of the net electric field Enet can be found using:
Enet=√E2net,x+E2net,y
Since Enet,x=Enet,y, we can simplify this to:
Enet=√2Enet,x
Substituting E+ and E− into the equations gives us the final expression for the electric field intensity at the center of the square.
The final expression for the electric field intensity at the center of the square is:
Enet=4kQl2
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Practice Problems
88 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions
51 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Four charges of same magnitude and same sign are placed at the corners of a square, of each side0⋅1m. What is electric field intensity at the center of the square?
View SolutionTwo point charges of +q each are placed at two diagonally opposite corners of a square. Another two point charges of -q charge each are placed at the two remaining corners. Take the edge length of square equal to l. Calculate (i) work needed to move these charges slowly from an infinite separation to this given configuration. (ii) Assume that four charges at corners of the square are held fixed. Another charge Q is to be moved from infinity to the centre of this square slowly. What additional work is required to do so?
View Solution
Knowledge Check
Five identical point charges +Q are placed at the five corners of a regular hexagon of edge length a. One corner is empty. Electric field intensity at the centre of the hexagon is
AZeroBQ4πε0d2, towards the empty cornerCQ4πε0d2, away from the empty cornerD5Q4πε0a2 towards the empty cornerFour idential charges each of charge q are placed at the corners of a square .Then at the centre of the square the resultant electric intensity E and the net electric potential V are
AE≠0,V=0BE=0,V=0CE=0,V≠0DE≠0,V≠0Four point charges −Q,−q,2q and 2Q are placed, one at each corner of the square. The relation between Q and q for which the potential at the centre of the square is zero is
A1qBQ=−qCQ=−1qDQ=q
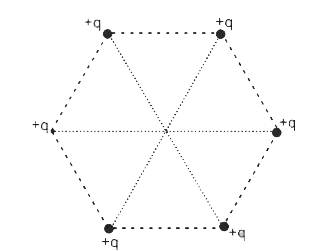
Six equal point charges are placed at the corners of a regular hexagon of side 'a'. Calculate electric field intensity at the centre of hexagon ?
View SolutionFour charges are placed at the corners of a square of side 10 cm as shown in figure. If q is 1μC, then what will be electric field intensity at the centre of the square?

View SolutionA positive charge Q is uniformly distributed along the length L of a rod. It is bent in the shape of a square. Calculate electric field intensity at the centre of the square.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionFour charges are arranged at the corners of a square as shown in the figure. The direction of electric field at the centre of the square is along

View Solution
