Two prisms A and B have dispersive powers of 0.012 and 0.018 respectively. The two prisms are in contact with each other. The prism A produces a mean deviation of 1.2∘, the mean deviation produced by B if the combination is achromatic is
3.6∘
0.8∘
0.4∘
1.8∘
The correct Answer is:B
To solve the problem, we need to find the mean deviation produced by prism B when the combination of prisms A and B is achromatic.
1. Understand the Given Data:
- Dispersive power of prism A, ωA=0.012
- Dispersive power of prism B, ωB=0.018
- Mean deviation produced by prism A, δA=1.2∘
- Mean deviation produced by prism B, δB (to be determined)
2. Condition for Achromatic Combination:
- For the combination to be achromatic, the total deviation must be zero:
θA+θB=0
- This implies that the deviations caused by the two prisms must balance each other out.
3. Relate Deviation to Dispersive Power:
- The deviation θ can be expressed in terms of the dispersive power and mean deviation:
θ=ω⋅δ
- Therefore, for prisms A and B, we have:
θA=ωA⋅δA
θB=ωB⋅δB
4. Set Up the Equation:
- Since the combination is achromatic:
θA+θB=0⟹ωA⋅δA+ωB⋅δB=0
- Rearranging gives:
ωA⋅δA=−ωB⋅δB
5. Substitute Known Values:
- Plugging in the values:
0.012⋅1.2=−0.018⋅δB
6. Solve for δB:
- Calculate 0.012⋅1.2:
0.012⋅1.2=0.0144
- Now, substituting back:
0.0144=0.018⋅δB
- Solving for δB:
δB=0.01440.018=0.8∘
Conclusion:
The mean deviation produced by prism B, when the combination is achromatic, is δB=0.8∘.
- Dispersive power of prism A, ωA=0.012
- Dispersive power of prism B, ωB=0.018
- Mean deviation produced by prism A, δA=1.2∘
- Mean deviation produced by prism B, δB (to be determined)
- For the combination to be achromatic, the total deviation must be zero:
θA+θB=0
- This implies that the deviations caused by the two prisms must balance each other out.
- The deviation θ can be expressed in terms of the dispersive power and mean deviation:
θ=ω⋅δ
- Therefore, for prisms A and B, we have:
θA=ωA⋅δA
θB=ωB⋅δB
- Since the combination is achromatic:
θA+θB=0⟹ωA⋅δA+ωB⋅δB=0
- Rearranging gives:
ωA⋅δA=−ωB⋅δB
- Plugging in the values:
0.012⋅1.2=−0.018⋅δB
- Calculate 0.012⋅1.2:
0.012⋅1.2=0.0144
- Now, substituting back:
0.0144=0.018⋅δB
- Solving for δB:
δB=0.01440.018=0.8∘
The mean deviation produced by prism B, when the combination is achromatic, is δB=0.8∘.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)7videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)9videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)17videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS10videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE106videos
LAWS OF MOTION
Similar Questions
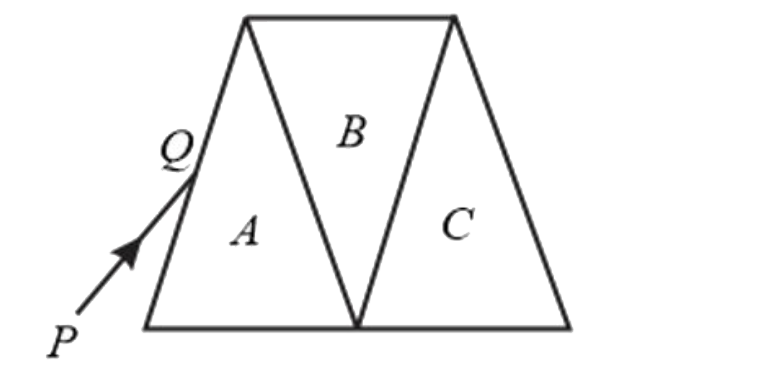
The ray PQ shown in the figure , surface minimum deviation in an equilateral prism A. Two more identical prism B and C and of the same material as A are now placed in contact as. Show in the figure . If prism A produces a minimum deviation δm, the deviation produced by the combination of prisms A, B and C will be
 View Solution
View SolutionA prism can produce a minmum deviation δ in a the beam. If three such prisms are combined, the minimum deviation that can be produced in this beam is
View SolutionTwo prisms A and B are in contact with each other have angular dispersions of 2∘ and 4∘ respectively. The dispersive power of A is 0.002. If the combination produces dispersion without deviation, the dispersive power of B is
View SolutionThe refractive indices of a material for red, violet and yellow colour lights are 1.52, 1.62 and 1.59 respectively. Calculate the dispersive power of the material. If the mean deviation is 40∘ what will be the angular dispersion produced by a prism of this material ?
View SolutionA thin prism of crown glass (μr=1.515,μv=1.525) and a thin prism of flint glass (μr=1.612,μv=1.632) are placed in contact with each other. Their refracting angles are 5.0∘ each and are similarly directed. Calculate the angular dispersion produced by the combination.
View SolutionTwo prisms of same glass (μ=√2) are stuck together without gap as shown. Find the angle of incidence i on the face AC such that the deviation produced by the combination is minimum ?
 View Solution
View SolutionTwo lenses have focal lengths f1 and f2 and their dispersive powers are ω1 and ω2 respectively. They will together form an achromatic combination if
View SolutionThe dispersive power (w) of the material of a prism is (where symbols have their usual meanings)
View SolutionThe dispersive powers of crown and flint glasses are 0.03 and 0.05 respectively, The refractive indices for yellow light for these glasses are 1.517 and 1.621 respectively. It is desired to from an achromatic combination of prisms of crown and flint glasses which can produce a deviation of 1∘ in the yellow ray. Find the refracting angles of the two prisms needed.
View SolutionIt is given that the disispersive powers of crown and flint glasses are 0.06 and 0.10 respectively. Also the refractive indices for yellow light for these glasses are 1.517 and 1.621, respectively. We have to form an achromatic combination of prism of crown and flint glasses which can produce a deviation of 1∘ in the yellow ray. Evaluate the refracting angles of the two prisms needed.
View Solution
