Two ships A and B are 4 km apart. A is due west of B. If A moves with a uniform velocity of 8 km hr−1 due east and B moves with a uniform velocity of 6 km hr−1 due south, calculate (i) the magnitude of velocity of A relative to B, (ii) the closest distance apart of A and B.
To solve the problem step by step, we will first analyze the velocities of ships A and B, and then calculate the required quantities.
Step 1: Understand the positions and velocities of the ships
- Ship A is initially located 4 km west of ship B.
- Ship A moves due east with a velocity of 8 km/hr.
- Ship B moves due south with a velocity of 6 km/hr.
Step 2: Determine the relative velocity of A with respect to B
The relative velocity of A with respect to B can be calculated using the formula:
→VA/B=→VA−→VB
Where:
- →VA is the velocity of A (8 km/hr east).
- →VB is the velocity of B (6 km/hr south).
Step 3: Represent the velocities as vectors
- The velocity of A can be represented as:
→VA=8^i km/hr(east direction)
- The velocity of B can be represented as:
→VB=−6^j km/hr(south direction)
Step 4: Calculate the relative velocity
Substituting the vectors into the relative velocity equation:
→VA/B=8^i−6^j
Step 5: Calculate the magnitude of the relative velocity
The magnitude of the relative velocity is given by:
|→VA/B|=√(8)2+(−6)2=√64+36=√100=10 km/hr
Step 6: Calculate the time taken for A to reach the position of B
The initial distance between A and B is 4 km. The relative velocity with which A approaches B is 10 km/hr. The time taken T for A to reach B is:
T=DistanceRelative Velocity=4 km10 km/hr=0.4 hours
Step 7: Calculate the distance traveled by B in that time
During the time T, ship B also moves south. The distance traveled by B in that time is:
Distance traveled by B=VB×T=6 km/hr×0.4 hr=2.4 km
Step 8: Calculate the closest distance between A and B
The closest distance apart of A and B occurs when A reaches the vertical line of B's initial position. The initial distance between A and B was 4 km, and B has moved 2.4 km south. Therefore, the closest distance D is:
D=4 km−2.4 km=1.6 km
Final Answers
1. The magnitude of the velocity of A relative to B is 10 km/hr.
2. The closest distance apart of A and B is 1.6 km.
- Ship A is initially located 4 km west of ship B.
- Ship A moves due east with a velocity of 8 km/hr.
- Ship B moves due south with a velocity of 6 km/hr.
The relative velocity of A with respect to B can be calculated using the formula:
→VA/B=→VA−→VB
Where:
- →VA is the velocity of A (8 km/hr east).
- →VB is the velocity of B (6 km/hr south).
- The velocity of A can be represented as:
→VA=8^i km/hr(east direction)
- The velocity of B can be represented as:
→VB=−6^j km/hr(south direction)
Substituting the vectors into the relative velocity equation:
→VA/B=8^i−6^j
The magnitude of the relative velocity is given by:
|→VA/B|=√(8)2+(−6)2=√64+36=√100=10 km/hr
The initial distance between A and B is 4 km. The relative velocity with which A approaches B is 10 km/hr. The time taken T for A to reach B is:
T=DistanceRelative Velocity=4 km10 km/hr=0.4 hours
During the time T, ship B also moves south. The distance traveled by B in that time is:
Distance traveled by B=VB×T=6 km/hr×0.4 hr=2.4 km
The closest distance apart of A and B occurs when A reaches the vertical line of B's initial position. The initial distance between A and B was 4 km, and B has moved 2.4 km south. Therefore, the closest distance D is:
D=4 km−2.4 km=1.6 km
1. The magnitude of the velocity of A relative to B is 10 km/hr.
2. The closest distance apart of A and B is 1.6 km.
Topper's Solved these Questions
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - NUMERICAL EXXERCISE (LEVEL -2)
21 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
Similar Questions
A ship A streams due north at 16kmh−1 and a ship B due west at 12kmh−1. At a certain instant B is 10km north east of A. Find the
(a) magnitude of velocity of Arelative→B.
(b) nearest distance of approach of ships.
View SolutionA car travels a distance 50 km with a velocity 25 km h−1 and then 60 km with a velocity 20 km h−1 in the same direction. Calculate : (i) the total time of journey and (ii) the average velocity of the car.
View SolutionA man moves on a cycle with a velocity of 4 km/hr. The rain appears to fall on him with a velocity of 3 km/hr vertically. The actual velocity of the rain is
View SolutionA motorcylcle is moving with a velocity 80km/hr ahead of a car moving with a velocity of 65 km/hr in the same direction. What is the relative velocity of the motorcyle with respect ot the car:-
View SolutionA man A moves due to East with velocity 6ms−1 and another man B moves in N−30∘E with 6ms−1 . Find the velocity of B w.r.t. A.
View SolutionA train first travels for 30 min with a velocity 30 km h−1 and then for 40 min with a velocity 40 km h−1 in the same direction, Calculate : (i) the total distance travelled, (ii) the average velocity of the train.
View SolutionA ship 'A' steams down to North at 16 km/h, and ship 'B' due west at 12 km/h. at a certain instant B is 10 km north east of A . find the magnitude of velocity of A relative to B?
View SolutionA bird is flying towards north with a velocity 40kmh−1 and a train is moving with velocity 40kmh−1 towards east. What is the velocity of the bird boted by a man in the train ?
View SolutionA car A moves with velocity 15ms−1 and B with velocity 20ms−1 are moving in opposite directions as shown in . Find the relative velocity of B w.r.t. A and w.r.t. B.
 .
.
View SolutionA boat is travelling with a speed of 27 km h−1 due east. An observer is situated at 30 m south of the line of travel. The angular velocity of the boat relative to be the observer in the position shown will be
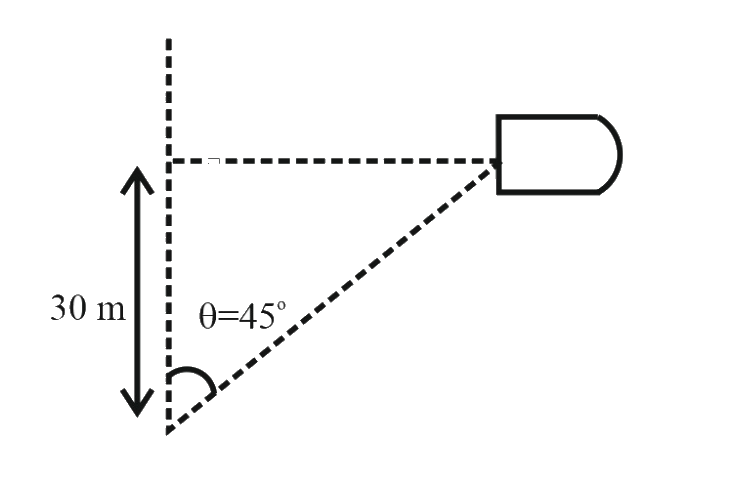
View Solution
