Two sources S1 and S2, each emitting waves of wavelength λ are kept symmetrically on either side of centre o of a circle ABCD such that S1O=S2O=2λ . If a detector is moved along the circumference of the circle, it will record how many maximum in one revolution
8
12
16
24
The correct Answer is:A
To solve the problem, we need to determine how many maxima will be observed by a detector moving along the circumference of the circle when two sources S1 and S2 are emitting waves of wavelength λ.
1. Understanding the Setup:
- We have two sources S1 and S2 placed symmetrically on either side of the center O of a circle.
- The distance from each source to the center O is given as S1O=S2O=2λ.
2. Path Difference:
- When the detector moves along the circumference of the circle, the path difference between the waves arriving from S1 and S2 at any point P on the circumference can be expressed as:
S2P−S1P
- For constructive interference (maxima), this path difference must be an integer multiple of the wavelength:
S2P−S1P=nλ(n=0,1,2,…)
3. Geometry of the Circle:
- The distance S1P and S2P can be expressed using the geometry of the circle. As the detector moves along the circumference, the path difference will vary.
4. Maximum Path Difference:
- The maximum path difference occurs when the detector is at points directly opposite to each source, which is when the path difference is maximized.
- The maximum path difference can be calculated as:
Max Path Difference=S2O+S1O=2λ+2λ=4λ
5. Finding the Number of Maxima:
- The condition for maxima is:
S2P−S1P=nλ
- The maximum path difference of 4λ allows for the following integer values of n:
n=0,1,2,3,4
- This gives us a total of 5 maxima in one complete revolution around the circle.
Conclusion:
Thus, the detector will record 5 maxima in one complete revolution around the circle.
---
- We have two sources S1 and S2 placed symmetrically on either side of the center O of a circle.
- The distance from each source to the center O is given as S1O=S2O=2λ.
- When the detector moves along the circumference of the circle, the path difference between the waves arriving from S1 and S2 at any point P on the circumference can be expressed as:
S2P−S1P
- For constructive interference (maxima), this path difference must be an integer multiple of the wavelength:
S2P−S1P=nλ(n=0,1,2,…)
- The distance S1P and S2P can be expressed using the geometry of the circle. As the detector moves along the circumference, the path difference will vary.
- The maximum path difference occurs when the detector is at points directly opposite to each source, which is when the path difference is maximized.
- The maximum path difference can be calculated as:
Max Path Difference=S2O+S1O=2λ+2λ=4λ
- The condition for maxima is:
S2P−S1P=nλ
- The maximum path difference of 4λ allows for the following integer values of n:
n=0,1,2,3,4
- This gives us a total of 5 maxima in one complete revolution around the circle.
Thus, the detector will record 5 maxima in one complete revolution around the circle.
Topper's Solved these Questions
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-IV (LEVEL-II(ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
6 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-IV (LEVEL-II(ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
1 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-III (LEVEL-II(ADVANCED) INTEGER TYPE QUESTIONS))
2 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
Similar Questions
Two identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
View SolutionFigure shows two coherent sources S1andS2which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire at large radius is placed in such a way that S1S2 lies in its plane and the middle point of S1S2, is at the centre of the wire. Find the angular positions 0 on the wire for which constructive interference takes place.
View SolutionTwo source of sound, S1 and S2, emitting waves of equal wavelength 2cm, are placed with a separation of 3cm between them. A detector can be moved on a line parallel to S1S2 and at a distance 24cm from it. Initially, the detecor is equidistant from the two sources. Assuming that the waves emitted by the sources are in phase, find the minimum distance through which the detector should be shifted to detect a minimum of sound.
View SolutionFollowing figures shows sources S1 and S2 that emits light of wavelength λ in all directions. The sources are exactly in phase and are separated by a distance equal to 1.5λ. If we start at the indicated start point and travel along path 1 and 2, the interference produce a maxima all along

View SolutionTwo sources of sound, S1andS2 , emitting waves of equal wavelength 20.0 cm, are placed with a separation of 20.0 cm between them. A detector can be moved on a line parallel to S1S2 and at a distance of 20.0 cm from P it. Initially, the detector is equidistant from the two sources. Assuming that the waves emitted by the sources are in phase, find the minimum distance through wffich the detector should be shifted to detect a minimum of sound.
View SolutionTwo sources S1andS2 emitting light of wave length 600 nm are placed a distance 1.0x10−2 cm apart. A detector can be moved on the litre line S1P which is perpendicular to S1S2. a.What would be the minimum and maximum path differrence at the detector as it is moved alog the line S1P? b. Locate the position of the farthest minimum detect.
View SolutionTwo coherent point sources S1andS2 emit light of wavelength λ. The separation between sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance on this line from S2 where a minimum of intensity occurs?
View SolutionAssertion: Distance between two coherent sources S1andS2 is 4λ. A large circle is drawn around these sources with centre of circle lying at centre of S1andS2. There are total 16 maxima on this circle.
Reason: Total number of minimas on this circle are less, compared to total number of maximas.
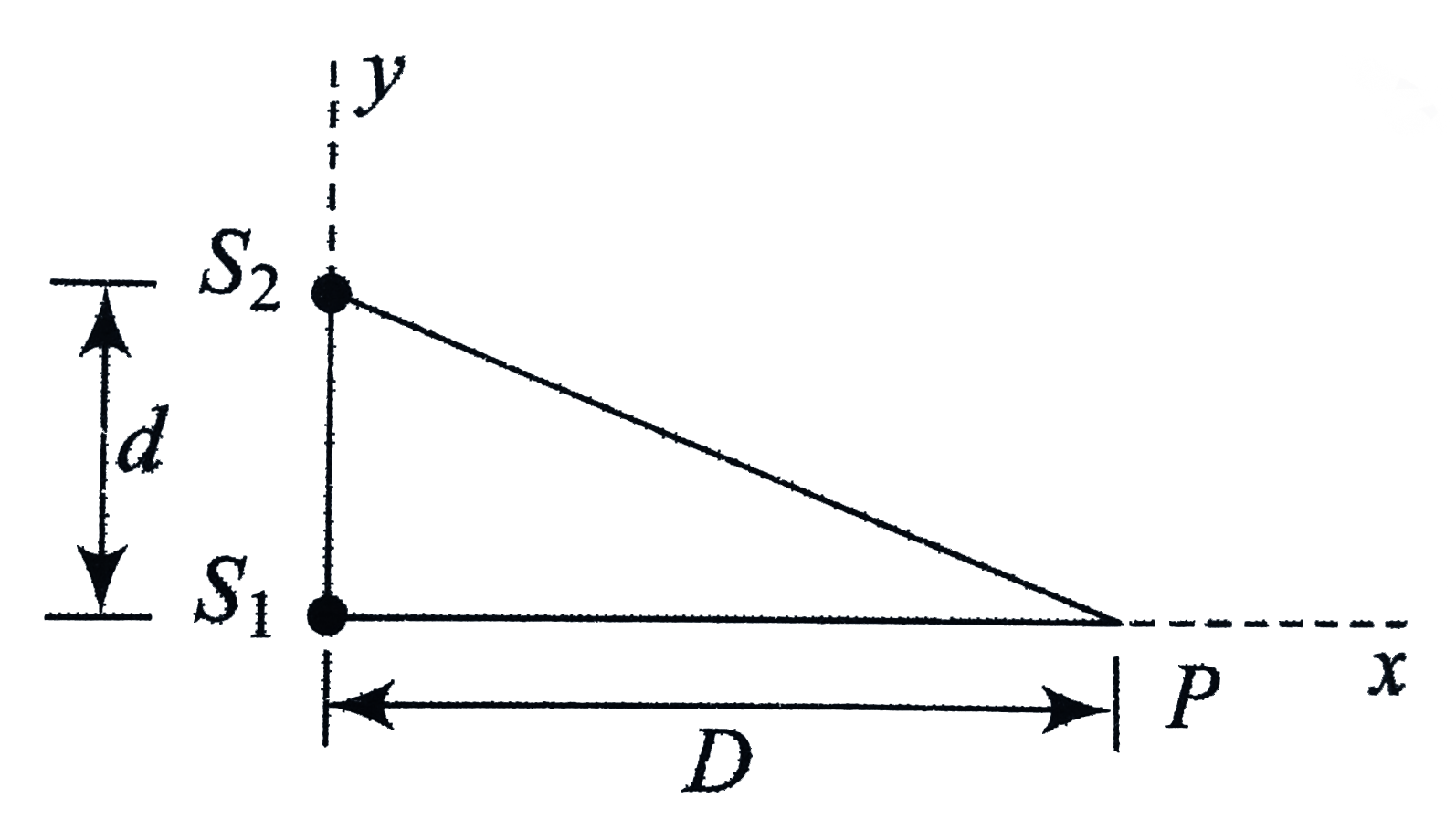
View SolutionTwo sources S1 and S2 emiting light of wavelenght 600 nm placed a distance 1.0×10−2 cm apart.
A detector can be moved on line S1P which is perpendicular to S1S2
(a) What would be the minimum and maximum path difference at the detector as it moves along line S1P ?
(b) Locate the psoition of the farthest minima detected
 .
.
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View Solution
