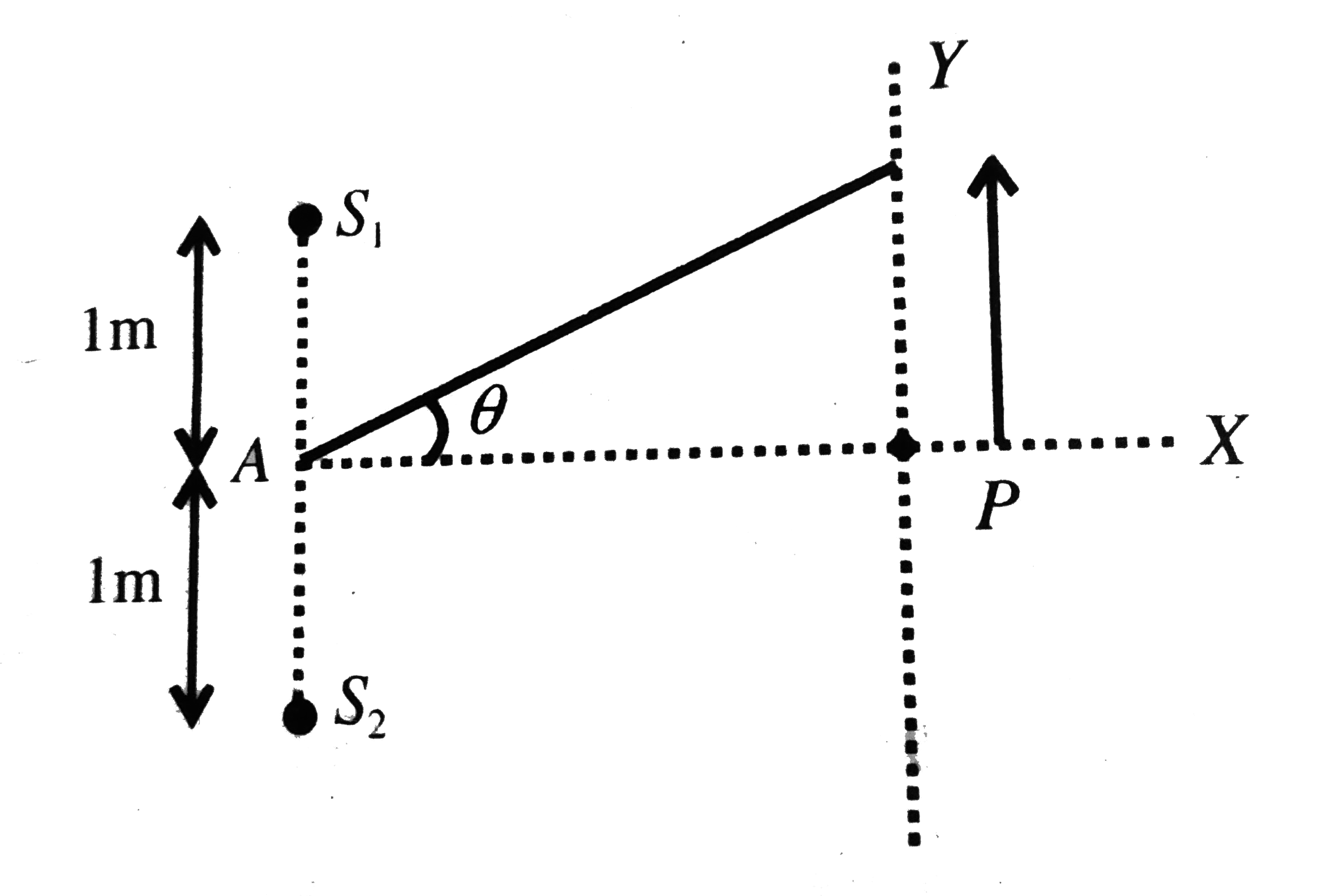
Two speakers derived by the same amplifier and placed at (Fig . 7.9) The speakers vibrate in phase at . A man stands at a point on the x - axis at a very large distance from the origin and starts moving parallel to the Y - axis . The speed of sound in air is .
(a). At what angle will the intensity of sound drop to a minimum for the first time ?
(b) At what angle will the sound intensity be maximum for the first time ?
(c ) If he continues to walk along the line , how many more maxima can he hear ?
The correct Answer is:A, B, C
Given
Let OP=D, PQ=y
…..i
Now path difference is given by
where d=2[the proof of x=(yd)/D
a.for minimum intensity
b. for minimum intensity
c. For more maxima
But since the maximum vlaue of theta can be he will hear two more maximum i.e. at .
Topper's Solved these Questions
Similar Questions
Circle(s) touching x-axis at a distance 3 from the origin and having an intercept of length 2√7 on y-axis is (are)
View SolutionTwo loudspeakers radiate in phase at 170HZ. An observer sits at 8m from one speaker and 11m from the other . The intensity level from either speaker acting alone is 60dB. The speed of sound is 340m/s. Find the observer intensity when both speakers are on together.
View Solution
Knowledge Check
- Question 1 - Select One
A train approaching a railway platform with a speed of 20 m s−1 starts blowing the whistle. Speed of sound in air is 340 ms−1. If the frequency of the emitted sound from the whistle is 640 Hz, the frequency of sound as heard by person standing on the platform
A600 HzB640 HzC680 HzD720 Hz
Two sound speakers are driver in phase by an audio amplifier at frequency 600HZ. The speed of sound is 340m/s. The speakers are on the y- axis, one at y=+1.0m and the other at y=−1.0m . A listener begins at y=0 and walks along a line parallel to the y - axis at a very large distance x away.
(a) At what angle θ (between the line from the origin to the listener at the x - axis) will she first hear a minimum sound intensity?
(b) At what angle will she first hear a maximum (afer θ=o∘) sound intensity?
(c ) How many maxima can she possible hear if she keeps walking in the same direction?View SolutionThe speed of sound in air is 330 ms−1 and in water is 1650 ms−1. It takes 2 s for sound to reach a certain distance from the source placed in air. Find the distance.
View SolutionThe speed of sound in air is 330 ms−1 and in water is 1650 ms−1. It takes 2 s for sound to reach a certain distance from the source placed in air. How much time will it take for sound to reach the same distance when the source is in water ?
View SolutionThe intensity of sound from a public loud speaker is 1μwatt m−2 at a distance of 5 m. What is the intensity at a distance of 100 m ?
View SolutionA plane passes through thee points P(4,0,0)andQ(0,0,4) and is parallel to the Y-axis. The distance of the plane from the origin is
View SolutionA body starts from the origin with an acceleration of 6ms−2 along the x - axis and 8ms−2 along the y - axis. Find its distance from the origin after 4s.
View SolutionA source of sound of frequency 600Hz is placed inside of water. The speed of sound is water is 1500m/s and air it is 300m/s. The frequency of sound recorded by an observer who is standing in air is
View Solution

