Two springs A and B(kA=2kB) are stretched by applying forces of equal magnitudes at the force ends. If the energy stored in A is E, that in B is
E2
2E
E
E4
The correct Answer is:B
To solve the problem, we need to find the energy stored in spring B when the energy stored in spring A is given as E, and we know the relationship between the spring constants of the two springs.
1. Understanding Spring Constants:
We know that the spring constants are related as kA=2kB. This means that spring A is stiffer than spring B.
2. Force Applied:
Both springs are stretched by applying forces of equal magnitude F. According to Hooke's Law, the force exerted by a spring is given by:
F=kx
where k is the spring constant and x is the elongation of the spring.
3. Elongation of Each Spring:
For spring A:
F=kAxA⟹xA=FkA
For spring B:
F=kBxB⟹xB=FkB
4. Energy Stored in Each Spring:
The potential energy stored in a spring is given by:
U=12kx2
For spring A:
UA=12kAx2A=12kA(FkA)2=F22kA
For spring B:
UB=12kBx2B=12kB(FkB)2=F22kB
5. Relating the Energies:
Since kA=2kB, we can express UA in terms of UB:
UA=F22kA=F22(2kB)=F24kB
Now substituting for UB:
UB=F22kB
6. Finding the Ratio of Energies:
Now, we can find the ratio of the energies:
UAUB=F24kBF22kB=1/41/2=12
Thus, we have:
UB=2UA
7. Final Result:
If the energy stored in spring A is E, then:
UB=2E
Conclusion:
The energy stored in spring B is 2E.
We know that the spring constants are related as kA=2kB. This means that spring A is stiffer than spring B.
Both springs are stretched by applying forces of equal magnitude F. According to Hooke's Law, the force exerted by a spring is given by:
F=kx
where k is the spring constant and x is the elongation of the spring.
For spring A:
F=kAxA⟹xA=FkA
For spring B:
F=kBxB⟹xB=FkB
The potential energy stored in a spring is given by:
U=12kx2
For spring A:
UA=12kAx2A=12kA(FkA)2=F22kA
For spring B:
UB=12kBx2B=12kB(FkB)2=F22kB
Since kA=2kB, we can express UA in terms of UB:
UA=F22kA=F22(2kB)=F24kB
Now substituting for UB:
UB=F22kB
Now, we can find the ratio of the energies:
UAUB=F24kBF22kB=1/41/2=12
Thus, we have:
UB=2UA
If the energy stored in spring A is E, then:
UB=2E
The energy stored in spring B is 2E.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -28videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Exercises64videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Worked out Examples14videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
Similar Questions
Two springs A and B (KA=2KB) are stretched by same suspended weights then ratio of workdone in stretching is -
View SolutionTwo springs have force constants kA such that kB=2kA. The four ends of the springs are stretched by the same force. If energy stored in spring A is E, then energy stored in spring B is
View Solution
Knowledge Check
- Question 1 - Select One
Two springs A and B are identical except that A is stiffer than B i.e., kA>kB. If the two springs are stretched by the same force, then
Amore work is done on B i.e., WB>WABmore work is done on A i.e., WA>WBCwork done on A and B are equalDwork done depends upon the way in which they are stretched - Question 2 - Select One
A long spring is stretched by 2 cm, its potential energy is U. IF the spring is stretched by 10 cm, the potential energy stored in it will be
AU/25BU/5C5 UD25 U
Two springs have their force constants in the ratio of 3:4. Both the springs are stretched by applying equal force F. If elongation in first spring is x then elogation is second spring is
View SolutionIn the following figure, if magnitude of forces between B and C is F, then magnitude of force between A and B is
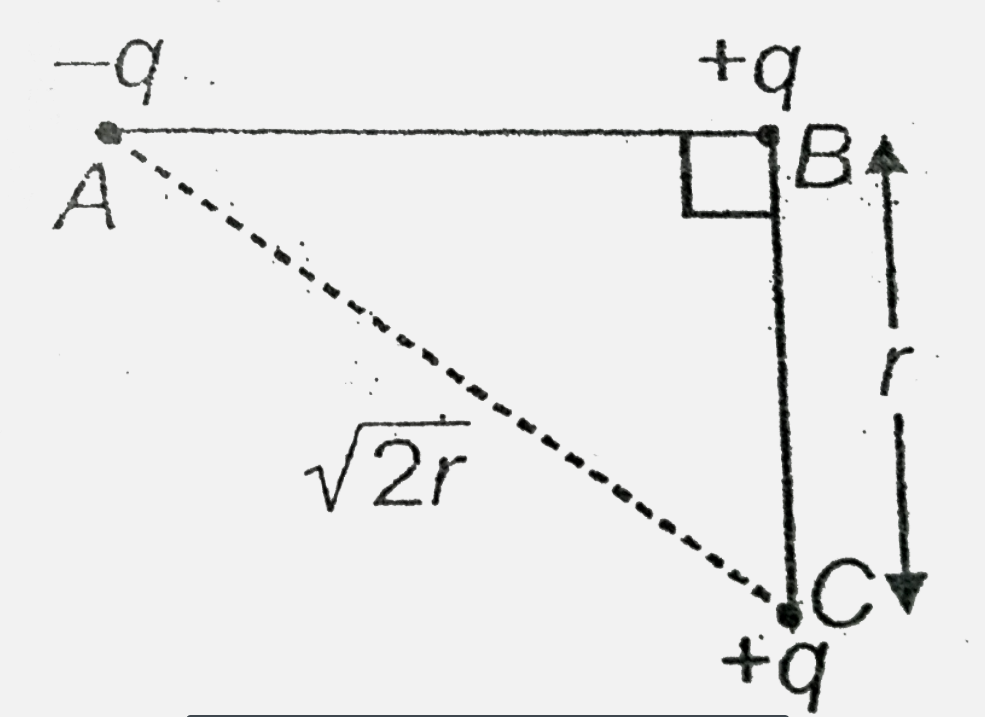 View Solution
View SolutionA spring of force constant k extends by a length X on loading . If T is the tension in the spring then the energy stored in the spring is
View SolutionForce constants K1andK2 of two springs are in the ratio 5:4. They are stretched by same length. If potential energy stored in one spring is 25 J then potential energy stored in second spring is
View SolutionTwo springs with spring constants K1=1500N/mand m K2=3000N/m are stretched by the same force. The ratio of potential energy stored in spring will be
View SolutionThe potential energy of a long spring when stretched by 2 cm is U. If the spring is stretched by 8 cm the potential energy stored in it is:-
View Solution

