Two trolleys and are free to move on a level frictionless track, and are initially stationary. A man on trolley throws a bag of mass with a horizontal velocity of with respect to himself on to trolley of mass . The combined mass of trolley (excluding bag) and the man is . Find the ratio of velocities of trolleys and , just after the bag lands on trolley .
To solve the problem, we will apply the principle of conservation of momentum. The steps are as follows:
Step 1: Understand the initial conditions
- Trolley A has a mass mA=140kg (combined mass of trolley A and the man).
- Trolley B has a mass mB=100kg.
- The bag has a mass mbag=10kg.
- The initial velocity of both trolleys is 0m/s.
Step 2: Determine the final velocities after the bag is thrown
Let v1 be the final velocity of trolley A after the bag is thrown, and v2 be the final velocity of trolley B after the bag lands on it.
Step 3: Apply conservation of momentum
Before the bag is thrown, the total momentum of the system is:
Initial momentum=0(since both trolleys are stationary)
After the bag is thrown, the momentum of the system can be expressed as:
Final momentum=mAv1+mBv2+mbag(v2+4)
Here, v2+4 is the velocity of the bag with respect to the ground after being thrown.
Setting the initial momentum equal to the final momentum gives us:
0=mAv1+mBv2+mbag(v2+4)
Step 4: Substitute the known values
Substituting the values into the equation:
0=140v1+100v2+10(v2+4)
This simplifies to:
0=140v1+100v2+10v2+40
0=140v1+110v2+40
Step 5: Rearranging the equation
Rearranging gives:
140v1+110v2=−40
Step 6: Express v1 in terms of v2
From the equation:
140v1=−40−110v2
v1=−40−110v2140
Step 7: Apply conservation of momentum for trolley B and the bag
For trolley B and the bag:
mBv2=mbag(v2+4)
Substituting the masses:
100v2=10(v2+4)
This simplifies to:
100v2=10v2+40
90v2=40
v2=4090=49m/s
Step 8: Substitute v2 back to find v1
Substituting v2 back into the equation for v1:
v1=−40−110(49)140
Calculating:
v1=−40−4409140
v1=−3609−4409140=−8009140=−8001260=−80126=−4063m/s
Step 9: Find the ratio of velocities v1v2
Now, we can find the ratio:
v1v2=−406349=−40⋅963⋅4=−360252=−6042=−107
Final Answer
The ratio of the velocities of trolleys A and B just after the bag lands on trolley B is:
v1v2=−107
- Trolley A has a mass mA=140kg (combined mass of trolley A and the man).
- Trolley B has a mass mB=100kg.
- The bag has a mass mbag=10kg.
- The initial velocity of both trolleys is 0m/s.
Let v1 be the final velocity of trolley A after the bag is thrown, and v2 be the final velocity of trolley B after the bag lands on it.
Before the bag is thrown, the total momentum of the system is:
Initial momentum=0(since both trolleys are stationary)
Final momentum=mAv1+mBv2+mbag(v2+4)
Here, v2+4 is the velocity of the bag with respect to the ground after being thrown.
0=mAv1+mBv2+mbag(v2+4)
Substituting the values into the equation:
0=140v1+100v2+10(v2+4)
This simplifies to:
0=140v1+100v2+10v2+40
0=140v1+110v2+40
Rearranging gives:
140v1+110v2=−40
From the equation:
140v1=−40−110v2
v1=−40−110v2140
For trolley B and the bag:
mBv2=mbag(v2+4)
Substituting the masses:
100v2=10(v2+4)
This simplifies to:
100v2=10v2+40
90v2=40
v2=4090=49m/s
Substituting v2 back into the equation for v1:
v1=−40−110(49)140
Calculating:
v1=−40−4409140
v1=−3609−4409140=−8009140=−8001260=−80126=−4063m/s
Now, we can find the ratio:
v1v2=−406349=−40⋅963⋅4=−360252=−6042=−107
The ratio of the velocities of trolleys A and B just after the bag lands on trolley B is:
v1v2=−107
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.324videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective23videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.120videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Two trolleys A and B are moving with accelerations a and 2a, respectively, in the same direction. To an observer in trolley A. Find the magnitude of the pseudo force acting on a block of mass m on trolley B.
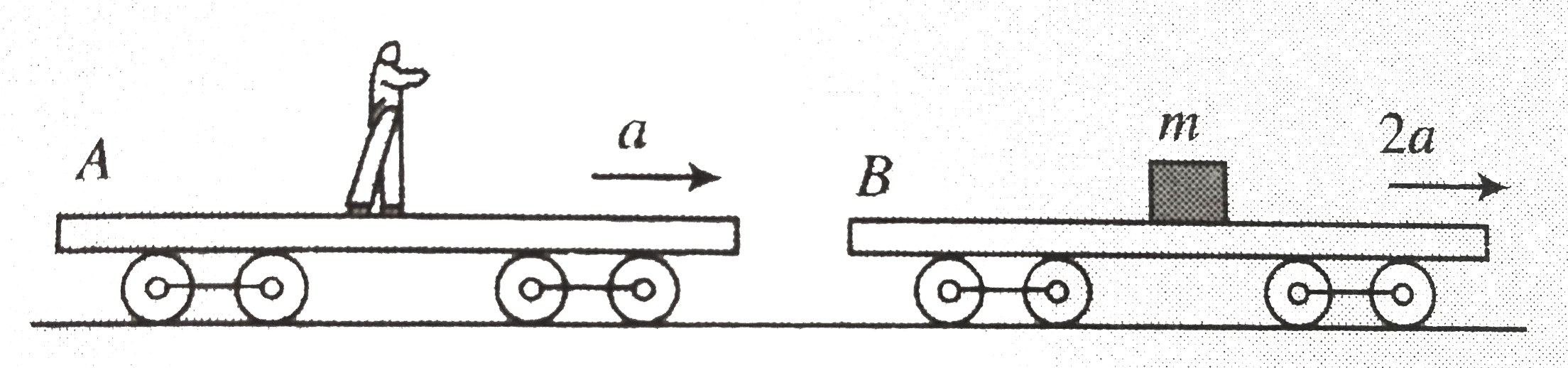 View Solution
View SolutionA shell of mass 10 kg is moving with a velocity with a velocity of 10ms−1 when it blasts and forms two parts of mass 9 kg and 1 kg respectively. If the 1st mass is stationary, the velocity of the 2nd is
View SolutionA body of mass 0.25 kg is projected with muzzle velocity 100ms−1 from a tank of mass 100 kg. What is the recoil velocity of the tank
View SolutionThe escape velocity for a body of mass 1 kg from the earth surface is 11.2kms−1. The escape velocity for a body of mass 100 kg would be
View SolutionAn object of mass 2kg is sliding with a constant velocity of 4ms−1 on a frictionless horizontal table. The force required to keep the object moving with the same velocity is
View SolutionA bomb of mass 12 kg explodes into two pieces of masses 4 kg and 8 kg. The velocity of mass 4 kg is 20 m/s. Find the velocity of mass 8 kg.
View SolutionA man of mass 60kg jumps from a trolley of mass 20kg standing on smooth surface with absolute velocity 3m/s. Find velocity of trolley and total energy produced by man.
View SolutionA constant force F is applied on a trolley of initial mass m0 kept over a smooth surface. Sand is poured gently over the trolley at a constant rate of (μ)kg//s. Afer time t, find

(a) mass of the trolley (with sand)
(b) net force on the trolley
(c) velocity of trolleyView SolutionTwo trolley 1 and 2 are moving with acceleration a1 and a2 respectively, in the same direction. A block of mass m on trolley 1 is in equilibrium from the frame of observer stationary with respect to trolley 2. the magnitude of friction force on block due to trolley is (assume taht no horizontal force other than friction force is acting on block).
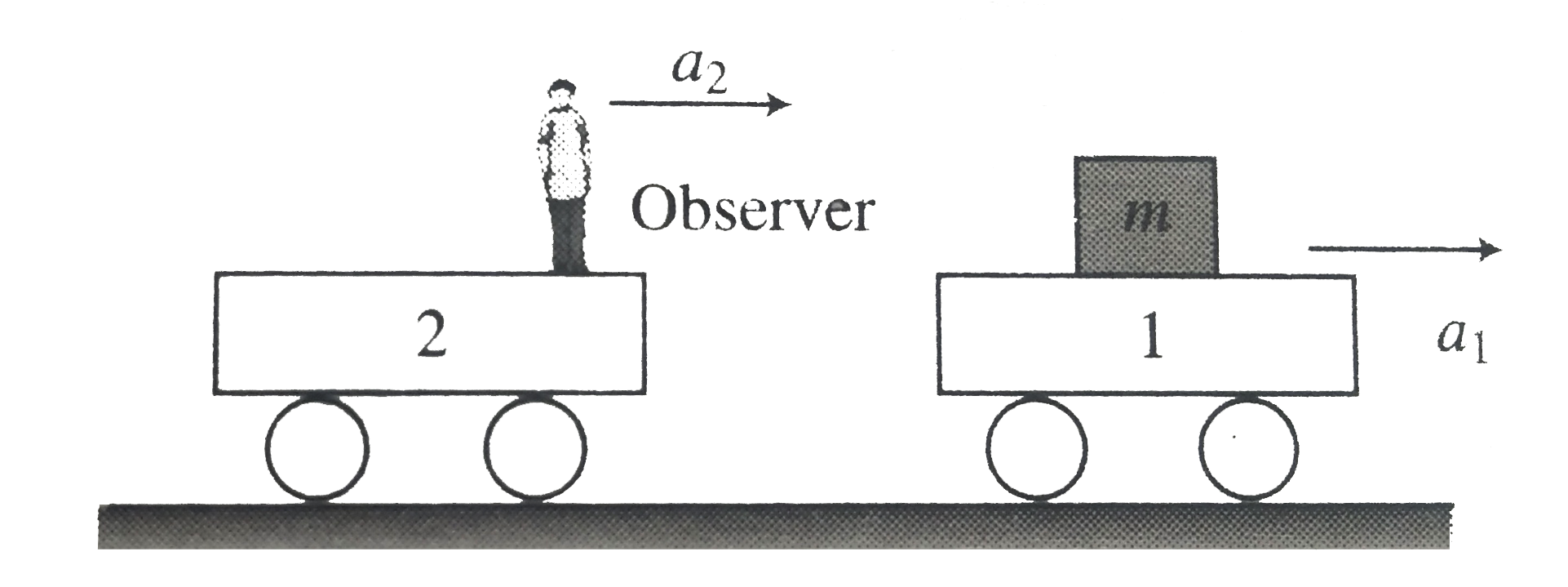 View Solution
View SolutionA block of mass m is pushed with a velocity v0 along the surface of a trolley car of mass M. If the horizontal ground is smooth and the coefficient of kinetic friction between the block of plank is μ. Find the minimum distance of relative sliding between the block and plank.
 View Solution
View Solution

