Two wave pulses identical in shape but inverted with respect to each other are produced at the two ends of a stretched string. At an instant when the pulses reach the middle, the string becomes completely straight. What happens to the energy of the two pulses ?
To solve the problem, we need to analyze the situation when two identical wave pulses, which are inverted with respect to each other, meet at the center of a stretched string.
1. Understanding Wave Pulses:
- We have two wave pulses that are identical in shape but inverted. This means that if one pulse is a crest, the other is a trough.
2. Movement Towards Each Other:
- The two pulses are produced at opposite ends of a stretched string and are moving towards each other.
3. Meeting Point:
- When the two pulses reach the middle of the string, they overlap completely.
4. Destructive Interference:
- Since the pulses are inverted, when they meet, they will undergo destructive interference. This means that the crest of one pulse cancels out the trough of the other pulse.
5. String Becomes Straight:
- At the point of destructive interference, the string becomes completely straight. This indicates that the net displacement of the string at that point is zero.
6. Energy Consideration:
- The energy carried by each pulse is related to the amplitude of the wave. When the pulses destructively interfere and the string becomes straight, the energy is not lost but rather transformed.
7. Energy Storage:
- The energy from the two pulses is stored as potential energy in the string. This is because the tension in the string remains, and the energy is temporarily stored in the form of potential energy due to the tension forces acting on the string.
8. Conclusion:
- Therefore, the energy of the two pulses does not disappear; instead, it gets stored in the string as potential energy during the moment of destructive interference.
Final Answer:
The energy of the two pulses gets stored in the form of potential energy when they meet and the string becomes completely straight due to destructive interference.
---
- We have two wave pulses that are identical in shape but inverted. This means that if one pulse is a crest, the other is a trough.
- The two pulses are produced at opposite ends of a stretched string and are moving towards each other.
- When the two pulses reach the middle of the string, they overlap completely.
- Since the pulses are inverted, when they meet, they will undergo destructive interference. This means that the crest of one pulse cancels out the trough of the other pulse.
- At the point of destructive interference, the string becomes completely straight. This indicates that the net displacement of the string at that point is zero.
- The energy carried by each pulse is related to the amplitude of the wave. When the pulses destructively interfere and the string becomes straight, the energy is not lost but rather transformed.
- The energy from the two pulses is stored as potential energy in the string. This is because the tension in the string remains, and the energy is temporarily stored in the form of potential energy due to the tension forces acting on the string.
- Therefore, the energy of the two pulses does not disappear; instead, it gets stored in the string as potential energy during the moment of destructive interference.
The energy of the two pulses gets stored in the form of potential energy when they meet and the string becomes completely straight due to destructive interference.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises57videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer9videos
THE FORCES
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer16videos
WORK AND ENERGY
Similar Questions
Two identical harmonic pulses travelling in opposite directions in a taut string approach each other. At the instant when they completely overlap, the total energy of the string will be
.View SolutionTwo wave pulses travel in opposite directions on a string and approch each other. The shape of the one pulse is same with respect to the other
View Solution
Knowledge Check
- Question 1 - Select One
A pulse of a wavetrain travels along a stretched string and reaches the fixed end of the string. It will be reflected back with
Aa phase change of 180∘ with velocity reversed.Bthe same phase as the incident pulse with no reversal of velocityCa phase change of 180∘ with no reversal of velocity.Dthe same phase as the incident pulse but with velocity reversed.
Two triangular wave pulses are travelling toward each other on a stretched string as shown in Fig . 7.25. Both pulses are identical to each other and travels at 2.00cm/s. The leading edges of the pulses are 1.00cmapart at t=0 . Sketch the shape of the string at t=0.250s,t=0.500s,t=0.750s,t=1.000sandt=1.250s.
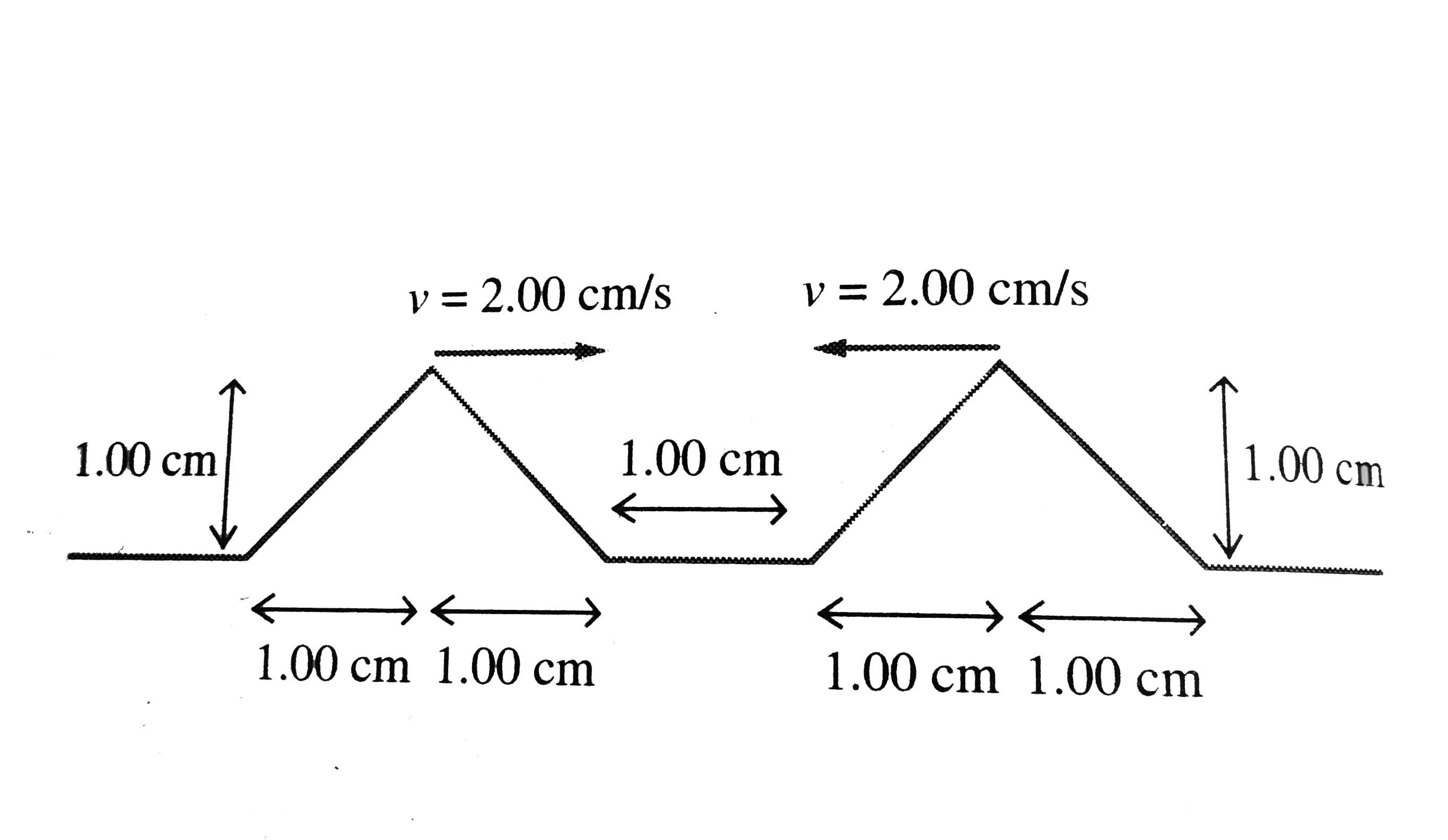View SolutionTwo pulses travel in mutually opposite directions in a string with a speed of 2.5cm/s as shown in the figure. Initially the pulses are 10cm apart. What will be the state of the string after two seconds?
View SolutionA triangular wave pulse moving at 2 cm/s on a rope approached an end at which it is free to slide on a vertical pole.
(a) Draw the pulse at 12s interval until it is completely reflected.
(b) What is the particle speed on the trailing edge P at the instant depicted?View SolutionTwo strings of copper are stretched to the same tension. If their cross-section area are in the ratio 1 : 4 , then the respective wave velocities will be
View SolutionTwo strings, A and B, of lengths 4L and L respectively and same mass M each, are tied together to form a knot 'O' and stretched under the same tension. A transverse wave puise is sent along the composite string from the side A, as shown to the right. Which of the following diagrams correctly shows the reflected and transmitted waves pulses near the knot 'O' ?
_S01_011_Q01.png)
View SolutionA particle of mass m1 is fastened to one end of a string and one of m2 to the middle point, the other end of the string being fastened to a fixed point on a smooth horizontal table The particles are then projected, so that the two portions of the string are always in the same straight line and describes horizontal circles find the ratio of tensions in the two parts of the string
View SolutionA series of pulses, each of amplitude 0.150m, are sent on a string that is attached to a wall at one end. The pulses are reflected at the wall and travel back along the string without loss of amplitude. When two waves are present on the same string. The net displacement of a given point is the sum of the displacement of the individuals waves at the point. What is the net displacement at point on the spring where two pulses am crossing, (a) if the string is rigidly attached to the post? (b) if the end at which reflection occurs is free is slide up and down ?
View Solution