When a particle is restricted to move along x-axis between x = 0 and x = 4, where a is of nanometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends r = 0 and x= a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de-Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p2/2m. Thus, the energy of the particle can be denoted by a quantum number 'r' taking values 1, 2, 3, ... (n = 1, called the ground state) corresponding to the number of loops in the standing wave. Use the model described above to answer the following three questions for a particle moving in the line x=0 to x=a. Take h=6.6×10−34Jsande=1.6×10−19C.
The allowed energy for the particle for a particular value of n is proportional to
a−2
a−3/2
a−1
a2
The correct Answer is:A
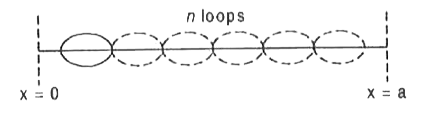
E=p22m, but according to de-Broglie theory.
λ=hporp=hλ
In this case, n loops are possible
p=nh2aasnλ2=a
E=(n2h24a2×2m)=n2h28ma2
Hence Eαn2 and E is also α1a2
Topper's Solved these Questions
- ATOMS, MOLECULES AND NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEIEXERCISE - MCQ (Level -II)
77 Videos
- ATOMS, MOLECULES AND NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEIEXERCISE - MCQ (Level -III)
9 Videos
- 15 MAGNETIC EFFECTS OF CURRENTSBOOK - MODERN PUBLICATIONCHAPTER - 15 MAGNETIC EFFECTS OF CURRENTSEXERCISE - Recent Competitive Questions
31 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - RECENT COMPETITIVE QUESTIONS
32 Videos
Similar Questions
When a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19 C.
Q. The allowed energy for the particle for a particular value of n is proportional to
View SolutionWhen a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19C
Q. The speed of the particle that can take discrete values is proportional to
View Solution
Knowledge Check
When a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19 C.
Q. The allowed energy for the particle for a particular value of n is proportional toAα−2Bα−32Cα−1Dα2When a particle is restricted to move aong xaxis between x=0 and x=a, where a is of nanometer dimension. Its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is realated to the linear momentum p of the particle according to the de Breogile relation. The energy of the particl e of mass m is reelated to its linear momentum as E=p22m. Thus, the energy of the particle can be denoted by a quantum number 'n' taking values 1,2,3,.......(n=1, called the ground state) corresponding to the number of loop in the standing wave.
Use the model decribed above to answer the following three questions for a particle moving in the line x=0 to x=a. Take h=6.6×10−34Js and e=1.6×10−19C.
The allowed energy for the particle for a particular value of n is proportional toAa−2Ba−3/2Ca−1Da2When a particle is restricted to move along x- axis between x=0andx=4 whwre a is opf nanometer demension , its energy can take only certain spscfic values . The allowed energies of the particles only in such a restiricted regain , correspond to the formation of standing wave with nodes at its end x=0andx=a.The wavelength of this standing wave is related to the linear momentum p of the paarticle according to the de Broglie relation .The energy of the particle of mass m is reated to its linear momentum as
E=p22m . thus , the energy of the particle can be denoted by a quantum number n taking value 1,2,3,....(n=1,cal≤dthegroundstate) corresponding to the number of loops in the standing wave use the model described above to answer the following there question for a particle moving in the line x=0→x=aTakeh=6.6×10−34Jsande=1.6×10−19C
The alloewd energy for the particle for a particular value of n is proportional toAa−2Ba−3/2Ca−1Da2
When a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19 C.
Q. If the mass of the particle is m=1.0×10−30kg and α=6.6nm, the energy of the particle in its ground state is closest to
View SolutionWhen a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19C
Q. The speed of the particle that can take discrete values is proportional to
View SolutionWhen a particle is restricted to move aong xaxis between x=0 and x=a, where a is of nanometer dimension. Its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is realated to the linear momentum p of the particle according to the de Breogile relation. The energy of the particl e of mass m is reelated to its linear momentum as E=p22m. Thus, the energy of the particle can be denoted by a quantum number 'n' taking values 1,2,3,.......(n=1, called the ground state) corresponding to the number of loop in the standing wave.
Use the model decribed above to answer the following three questions for a particle moving in the line x=0 to x=a. Take h=6.6×10−34Js and e=1.6×10−19C.
The speed of the particle, that can take disrete values, is proportional to
View SolutionWhen a particle is restricted to move along x- axis between x=0andx=4 whwre a is opf nanometer demension , its energy can take only certain spscfic values . The allowed energies of the particles only in such a restiricted regain , correspond to the formation of standing wave with nodes at its end x=0andx=a.The wavelength of this standing wave is related to the linear momentum p of the paarticle according to the de Broglie relation .The energy of the particle of mass m is reated to its linear momentum as
E=p22m . thus , the energy of the particle can be denoted by a quantum number n taking value 1,2,3,....(n=1,cal≤dthegroundstate) corresponding to the number of loops in the standing wave use the model described above to answer the following there question for a particle moving in the line x=0→x=aTakeh=6.6×10−34Jsande=1.6×10−19C
The speed of the particle , that can take discrete values, is propotional to
View SolutionWhen a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19 C.
Q. If the mass of the particle is m=1.0×10−30kg and α=6.6nm, the energy of the particle in its ground state is closest to
View Solution
