When a perosn throws a meter stivk it is found that the centre of the stick is moving with speed 10m/s and left end stick with speed 20m/s. Both points move vertically upwards at that moment. Then angular speed the stick is :
20rad/s
10rad/s
30rad/s
None of these
The correct Answer is:A
To find the angular speed of the meter stick when it is thrown, we can follow these steps:
Step 1: Understand the given information
- The center of the stick is moving with a speed of vcm=10m/s.
- The left end of the stick is moving with a speed of vL=20m/s.
- The length of the stick is L=1m.
Step 2: Determine the speed of the right end of the stick
Since the stick is uniform and the center of mass is at the midpoint, we can denote the speed of the right end as vR. The center of mass speed can be expressed as the average of the speeds of the two ends:
vcm=vL+vR2
Substituting the known values:
10=20+vR2
Step 3: Solve for vR
Multiply both sides by 2 to eliminate the fraction:
20=20+vR
Now, isolate vR:
vR=20−20=0m/s
Step 4: Calculate the angular speed
The angular speed ω can be calculated using the formula:
ω=vL−vRR
Where R is the distance from the center of mass to either end of the stick. Since the stick is 1 meter long, the distance from the center to either end is:
R=L2=12=0.5m
Substituting the values into the angular speed formula:
ω=20−00.5
Step 5: Simplify the expression
ω=200.5=40rad/s
Conclusion
The angular speed of the stick is 40rad/s.
- The center of the stick is moving with a speed of vcm=10m/s.
- The left end of the stick is moving with a speed of vL=20m/s.
- The length of the stick is L=1m.
Since the stick is uniform and the center of mass is at the midpoint, we can denote the speed of the right end as vR. The center of mass speed can be expressed as the average of the speeds of the two ends:
Multiply both sides by 2 to eliminate the fraction:
The angular speed ω can be calculated using the formula:
ω=200.5=40rad/s
The angular speed of the stick is 40rad/s.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
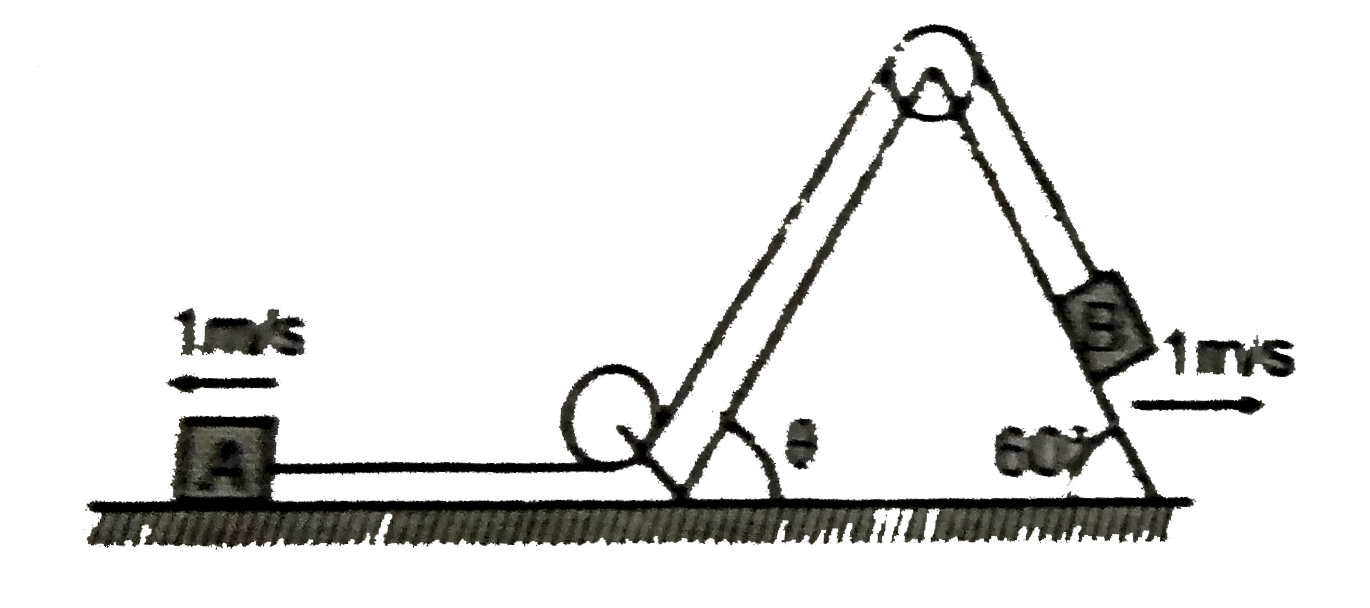
A system is shown in the figure. Block A is moving with 1m/s towards left. Wedge is moving with 1m/s towards right. Then speed of the block B will be :
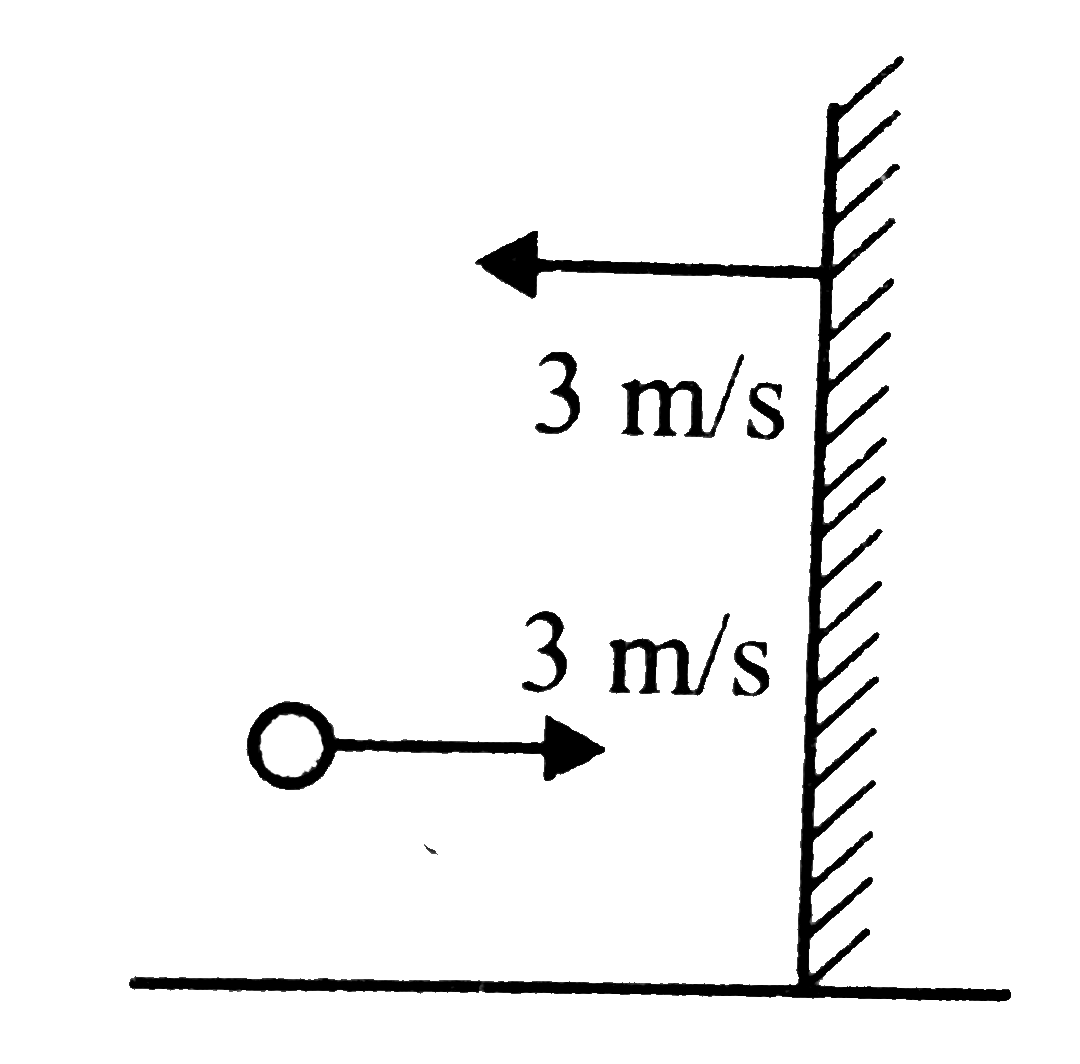
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
View Solutiontruck is moving with a speed of 15 m/s. A car chasing this truck with a speed of 10 m/s fires a bullet at truck with muzzle velocity 90 km/h. The speed with which the bullet hit the truck is
View SolutionA metre stick is pivoted about its centre. A piece of wax of mass 20 g travelling horizontally and perpendicular to it at 5 m/s strikes and adheres to one end of the stick so that the stick starts to rotate in a horizontal circle. Given the moment of inertia of the stick and wax about the pivot is 0.02 kg m2, the initial angular velocity of the stick is :
View SolutionSpeed of an object moving in cirular path of radius 10 m with angular speed 2 rad/s is
View SolutionA car moves a distance of 100 m. It coveres first half with speed of 10 m/s and another half with speed of v m/s. If the average speed of car is 18 m/s, then value of v is
View SolutionA rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of 45∘ and sticks to it. The angular velocity of system after collision is-
View SolutionA ball is thrown upward with speed 10 m/s from the top to the tower reaches the ground with a speed 20 m/s. The height of the tower is [Take g=10m/s2]
View SolutionA man standing on the edge of the terrace of a high rise building throws a stone, vertically up with at speed of 20m/s. Two seconds later, an identical stone is thrown vertically downwards with the same speed of 20m,. Then
View SolutionA car is moving at a speed of 40 m/s on a circular track of radius 400 m. this speed is increasing at the rate of 3 m/s2. The acceleration of car is
View Solution
