When a resistance of 11 Ω is connected in series with an electric cell, 0.5 A current flows thrugh it . If the 11 Ω resistor is replaced by 5Ω resistor the current flowing through it is 0.9 A . Find the internal resistance of the cell.
To find the internal resistance of the cell, we can follow these steps:
Step 1: Write down the formula for current in a circuit
The current I flowing through a circuit with an electromotive force (emf) E, an external resistance R, and an internal resistance r can be expressed as:
I=ER+r
Step 2: Set up the equations for both scenarios
1. For the first scenario with an 11 Ω resistor:
- Current I1=0.5A
- Resistance R1=11Ω
- The equation becomes:
0.5=E11+r(Equation 1)
2. For the second scenario with a 5 Ω resistor:
- Current I2=0.9A
- Resistance R2=5Ω
- The equation becomes:
0.9=E5+r(Equation 2)
Step 3: Rearrange both equations to express E
From Equation 1:
E=0.5(11+r)(1)
From Equation 2:
E=0.9(5+r)(2)
Step 4: Set the two expressions for E equal to each other
Since both expressions equal E, we can set them equal:
0.5(11+r)=0.9(5+r)
Step 5: Expand and simplify the equation
Expanding both sides:
5.5+0.5r=4.5+0.9r
Step 6: Rearrange to isolate r
Rearranging gives:
5.5−4.5=0.9r−0.5r
1=0.4r
Step 7: Solve for r
Dividing both sides by 0.4:
r=10.4=2.5Ω
Final Answer
The internal resistance of the cell is r=2.5Ω.
---
The current I flowing through a circuit with an electromotive force (emf) E, an external resistance R, and an internal resistance r can be expressed as:
I=ER+r
1. For the first scenario with an 11 Ω resistor:
- Current I1=0.5A
- Resistance R1=11Ω
- The equation becomes:
0.5=E11+r(Equation 1)
- Current I2=0.9A
- Resistance R2=5Ω
- The equation becomes:
0.9=E5+r(Equation 2)
From Equation 1:
E=0.5(11+r)(1)
E=0.9(5+r)(2)
Since both expressions equal E, we can set them equal:
0.5(11+r)=0.9(5+r)
Expanding both sides:
5.5+0.5r=4.5+0.9r
Rearranging gives:
5.5−4.5=0.9r−0.5r
1=0.4r
Dividing both sides by 0.4:
r=10.4=2.5Ω
The internal resistance of the cell is r=2.5Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
12 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
12 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
Similar Questions
When a resistor of 11Ω is connected in series with an electric cell, the current following in it is 0.5A. Instead, when a resistor of 5Ω is connected to the same electric cell in series, the current increases by 0.4A The internal resistance of the cell is
View SolutionCurrent through the 5Ω resistor is
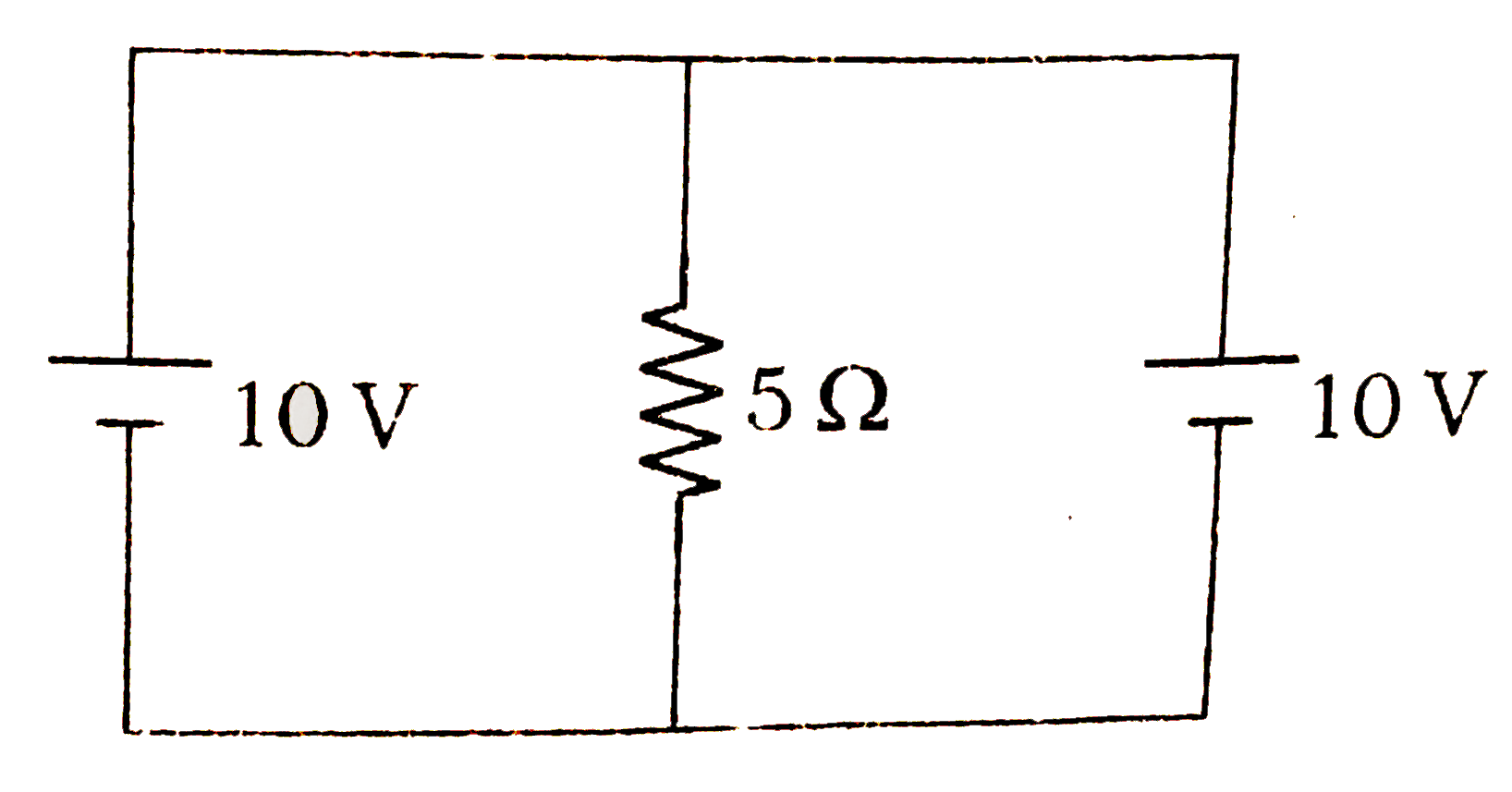
View Solution
Knowledge Check
A current of 3A flows through the 2Ω resistor as shown in the circuit. The power dissipated in the 5Ω resistor is
 A5 watt.B4 watt.C2 watt.D1 watt
A5 watt.B4 watt.C2 watt.D1 watt
A 50V battery is connected across a 10 ohm resistor. The current is 4.5A is flowing through the resistor then the internal resistance of the battery is
View SolutionIn the circuit, the current flowing through 10Ω resistance is
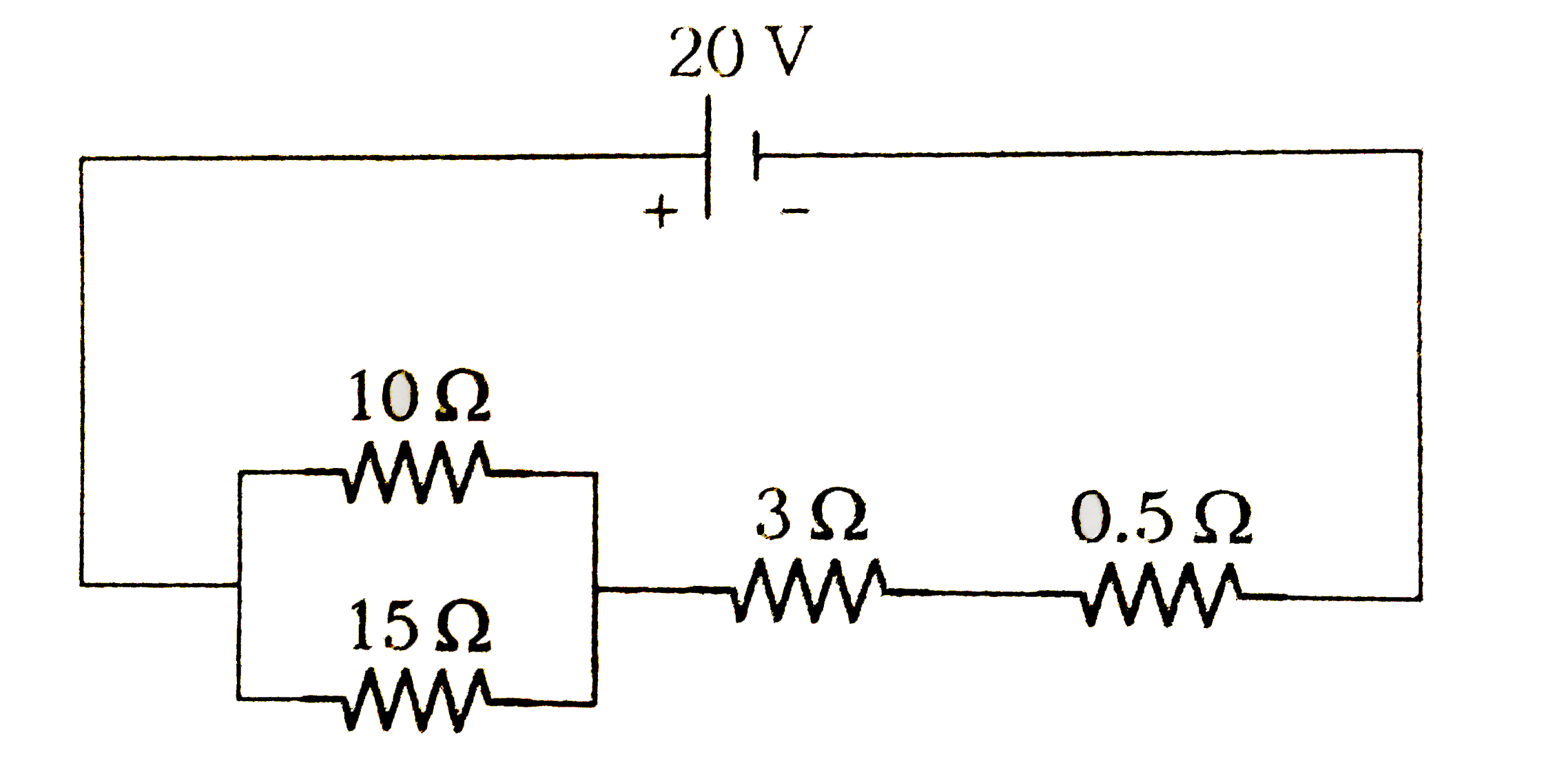
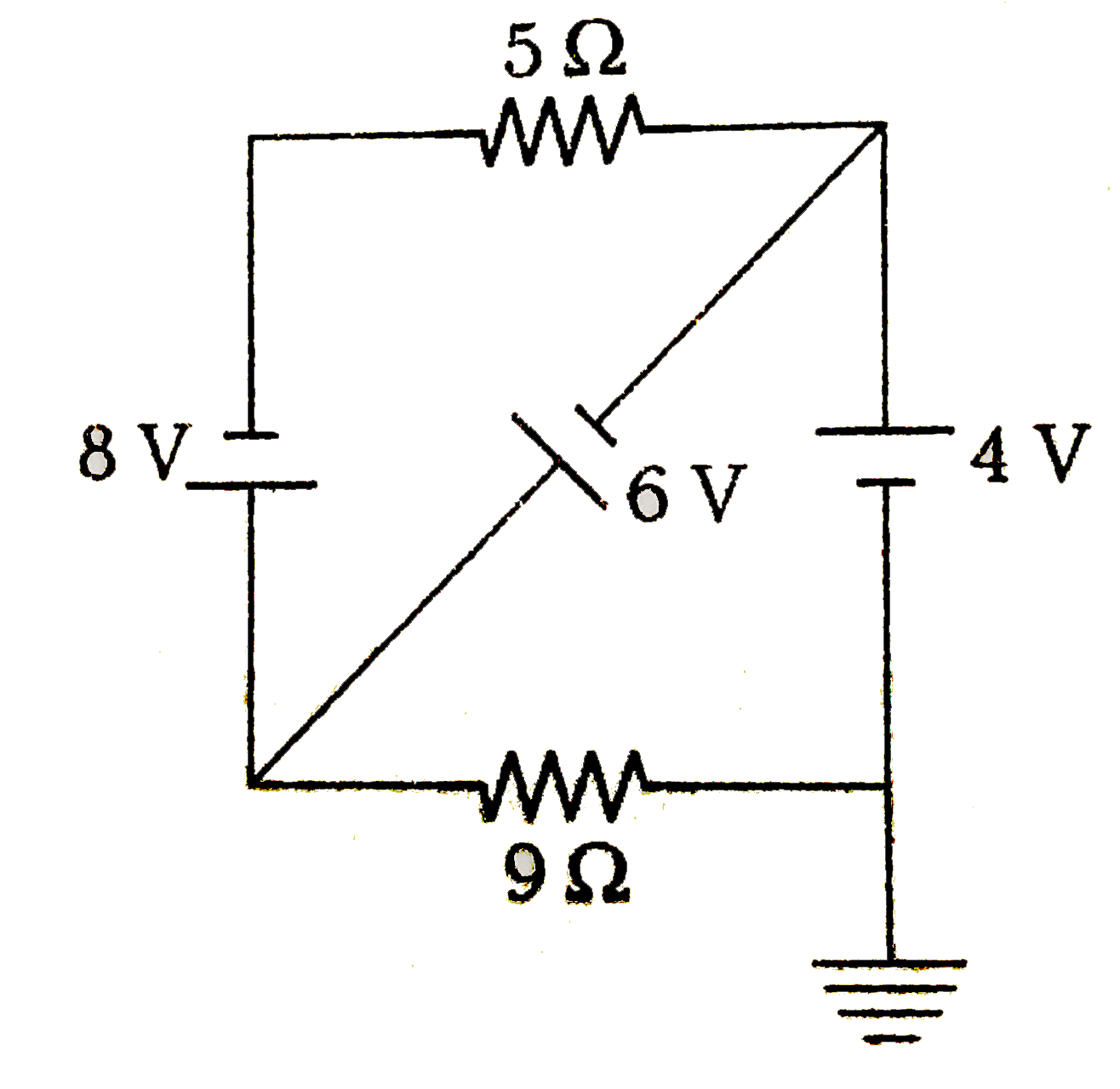
View SolutionThe current through the 5Ω resistor is
View SolutionCalculate the current flows through resistance 2Ω.
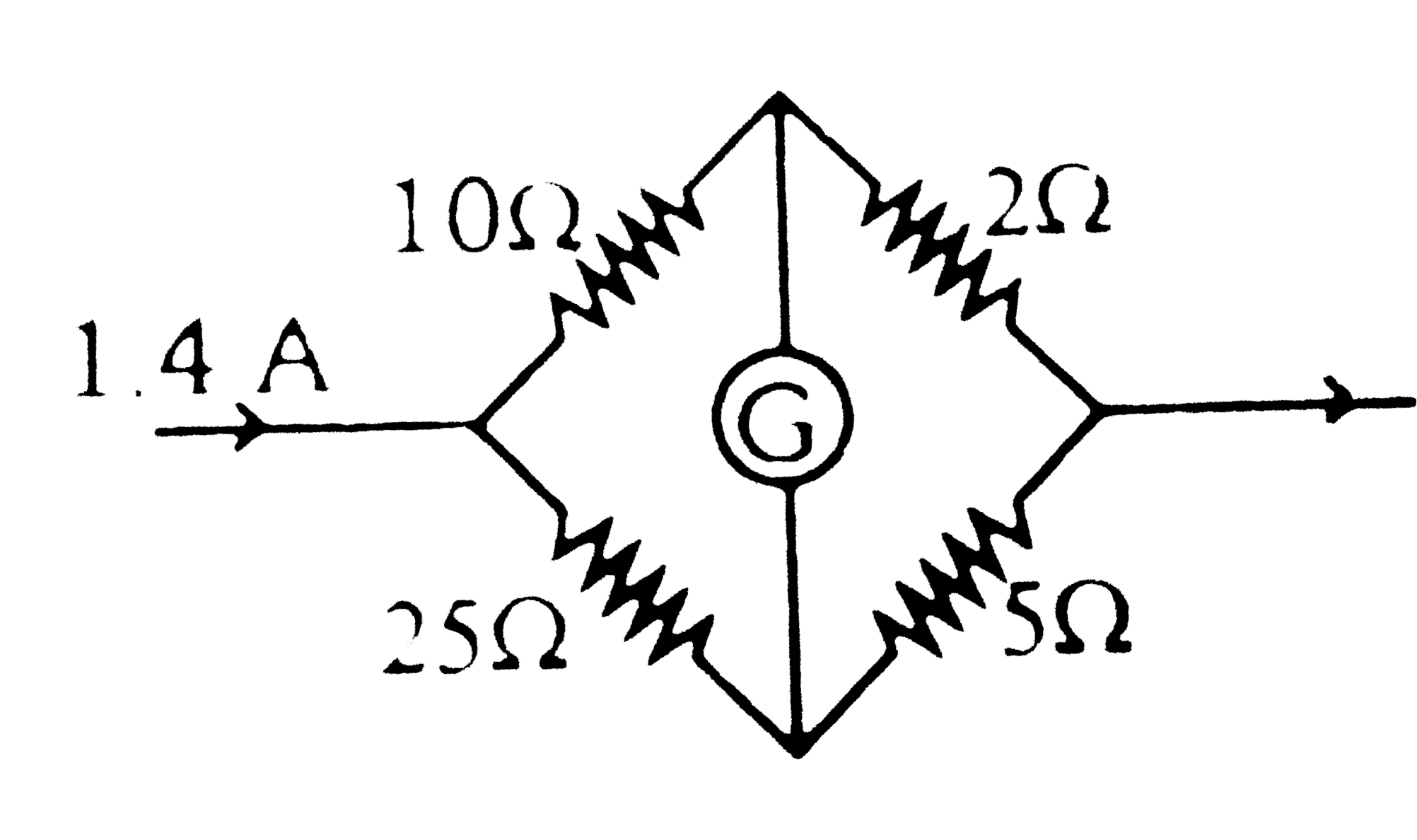
View Solution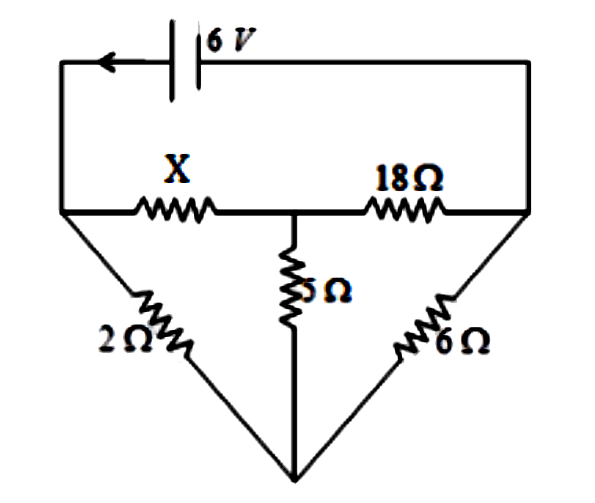
The magnitude of resistance X in the circuit shown in the given figure , when no current flows through the 5Ω resistor is
View Solutionn identical cells each of emf 6 V , connected in series with an external resistor of 5Ω, carry a current of 10A. If two cells are connected wrongly in series with the same external resistor, the current flowing through the cells will be 8A. Find the value of n and r the internal resistance of each cell.
View SolutionIn the given electric circuit if the current flowing through 3Ω resistor is 1 A, find the voltage of the battery and the current I drawn from it.

View Solution
