When forces F1 , F2 , F3 are acting on a particle of mass m such that F2 and F3 are mutually prependicular, then the particle remains stationary. If the force F1 is now rejmoved then the acceleration of the particle is
F2m
F2F3mF1
F2−F3m
F1m
The correct Answer is:D
Since the particle remains at rest under the action of
→F1,→F2and→F3
∴→F1=−(→F2+→F3)
→F1 is the equilibrant force.
When →F1 is removed, the resultant of →F2and→F3 has a magnitude of →F1.
∴ Acceleration of the particle =F1m and its direction is opposite to that of →F1.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
When forces F1, F2, F3, are acting on a particle of mass m such that F2 and F3 are mutually perpendicular, then the particle remains stationary. If the force F1 is now removed then the acceleration of the particle is
A(a) F/mB(b) F2F3/mF1C(c) (F2−F3)/mD(d) F2/m - Question 2 - Select One
When force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
A→F1/mB→F1/mC→F2−→F3/mD→F2/m - Question 3 - Select One
When force −→F1,−→F2,−→F3…...−→Fn act on a particle , the particle remains in equilibrium . If −→F1 is now removed then acceleration of the particle is
A−→F1mB−−→F1mC−−→F2+−→F3+.....−→Fn−−→F1mD−→F1m
F1 particle of oxysome
View SolutionFive forces →F1,→F2,→F3,→F4 , and →F5 , are acting on a particle of mass 2.0kg so that is moving with 4m/s2 in east direction. If →F1 force is removed, then the acceleration becomes 7m/s2 in north, then the acceleration of the block if only →F1 is action will be:
View SolutionWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
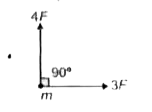 View Solution
View SolutionTwo forces f1=4N and f2=3N are acting on a particle along positve X−axis and negative y−axis respectively. The resultant force on the particle will be−
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View Solution

