When slow neutrons are incident on a target containing $235 . 92 U$ , a possible fission reaction is
$235 . 92 U + 1 . 0 n \to 141 . 56 B a + 92 . 36 K r + 3_{0}^{1} n$
Estimate the amount of energy released using the following data Given, mass of $235 . 92 U = 235.04 a μ$ , mass of $1 . 0 n = 1.0087 a μ$ , mass of $141 . 56 B a = 140.91 a μ$ , mass of $92 . 36 K r = 91.926 a μ$ , and energy equivalent to 1 amu=931 MeV.

Video Solution

Text Solution

Verified by Experts

$235 . 92 U + 1 . 0 n \to 141 . 56 B a + 92 . 36 K r + 3 1 . 0 n$
Total initial mass $(235 . 92 U + 1 . 0 n)$ =235.04+1.0087=236.0487 amu
Total final mass $(141 . 56 B a + 92 . 36 K r + 3 1 . 0 n) = 140.91 + 91926 + 3 \times 10087 = 235.8621 a μ$
Decrease in mass, $Δ m = 236.0487 - 235.8621 = 0.1866 a μ$
Energy released = $Δ m \times 931 = 0.1866 \times 931 = 173.725 M e V$

Updated on:21/07/2023

The end product of following reaction is

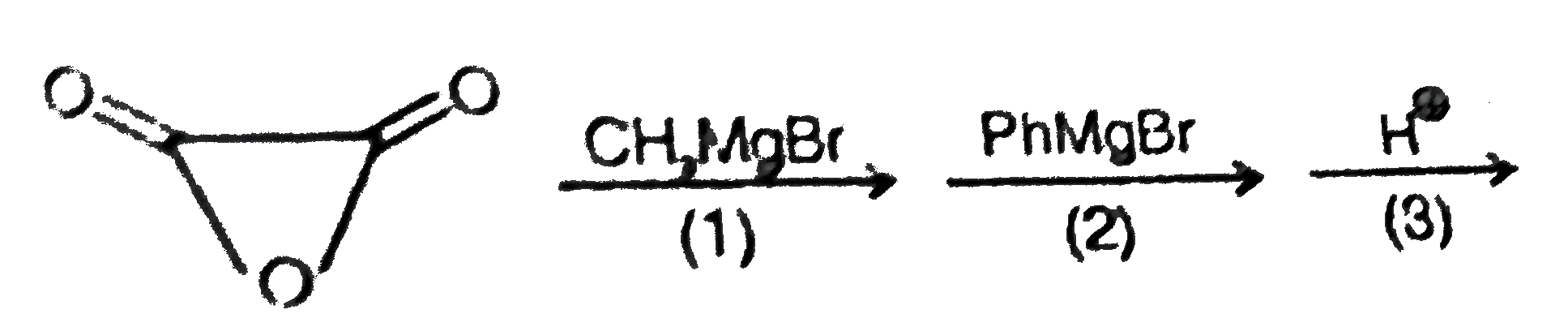
$C H_{3} M g B r - ---- \to (1) P h M g B r - --- \to (2) H^{\oplus} - - \to (3)$
A $α, β$ -diketone
B $α$ -Hydroxy acid
C1,2-Diol
D $β$ -Hydroxy acid
$3 Σ n = 1 \frac{{tan}^{- 1} 1}{n} =$
A0
B $π / 2$
C $π$
Dnone
In the reaction $2 . 1 H + 3 . 1 H \to 4 . 2 H e + 1 . 0 n .$ if the binding energies of $2 . 1 H, 3 . 1 H$ and $4 . 2 H e$ are respectively a , b and c (in MeV ) then the energy (in Me V) released in this reactions is
A $a + b + c$
B $c + a - b$
C $c - a - b$
D $a + b + c$