Write an expression for potential energy of two charges q1andq2at→r1and→r2 in a uniform electric field →E.
To find the expression for the potential energy of two charges q1 and q2 located at positions →r1 and →r2 in a uniform electric field →E, we can follow these steps:
Step 1: Understand the Electric Potential
In a uniform electric field →E, the electric potential V at a point →r can be expressed as:
V(→r)=−→E⋅→r+V0
where V0 is the reference potential at a chosen point.
Step 2: Calculate the Electric Potential at →r1 and →r2
For the two charges located at →r1 and →r2, the electric potentials V1 and V2 can be expressed as:
V1=−→E⋅→r1+V0
V2=−→E⋅→r2+V0
Step 3: Calculate the Potential Energy of Each Charge
The potential energy U of a charge q in an electric potential V is given by:
U=qV
Thus, the potential energy of charge q1 at →r1 is:
U1=q1V1=q1(−→E⋅→r1+V0)
And for charge q2 at →r2:
U2=q2V2=q2(−→E⋅→r2+V0)
Step 4: Total Potential Energy of the System
The total potential energy Utotal of the system is the sum of the potential energies of both charges:
Utotal=U1+U2=q1(−→E⋅→r1+V0)+q2(−→E⋅→r2+V0)
This simplifies to:
Utotal=−q1(→E⋅→r1)−q2(→E⋅→r2)+(q1+q2)V0
Step 5: Include the Interaction Energy
In addition to the potential energy due to the electric field, we must also consider the interaction energy between the two charges, which is given by:
Uinteraction=q1q24πϵ0|→r1−→r2|
Final Expression
Thus, the total potential energy of the system of two charges in a uniform electric field is:
Utotal=−q1(→E⋅→r1)−q2(→E⋅→r2)+(q1+q2)V0+q1q24πϵ0|→r1−→r2|
In a uniform electric field →E, the electric potential V at a point →r can be expressed as:
V(→r)=−→E⋅→r+V0
where V0 is the reference potential at a chosen point.
For the two charges located at →r1 and →r2, the electric potentials V1 and V2 can be expressed as:
V1=−→E⋅→r1+V0
V2=−→E⋅→r2+V0
The potential energy U of a charge q in an electric potential V is given by:
U=qV
Thus, the potential energy of charge q1 at →r1 is:
U1=q1V1=q1(−→E⋅→r1+V0)
And for charge q2 at →r2:
U2=q2V2=q2(−→E⋅→r2+V0)
The total potential energy Utotal of the system is the sum of the potential energies of both charges:
Utotal=U1+U2=q1(−→E⋅→r1+V0)+q2(−→E⋅→r2+V0)
This simplifies to:
Utotal=−q1(→E⋅→r1)−q2(→E⋅→r2)+(q1+q2)V0
In addition to the potential energy due to the electric field, we must also consider the interaction energy between the two charges, which is given by:
Uinteraction=q1q24πϵ0|→r1−→r2|
Thus, the total potential energy of the system of two charges in a uniform electric field is:
Utotal=−q1(→E⋅→r1)−q2(→E⋅→r2)+(q1+q2)V0+q1q24πϵ0|→r1−→r2|
Similar Questions
Knowledge Check
Force →F acting on a test charge q0 in a uniform electric field →E is
A→F=q0→EB→F=→Eq0C→F=q0→ED→F=q20→EForce →F acting on a test charge q0 in a uniform electric field →E is
A→F=q0→EB→F=→Eq0C→F=q0→ED→F=q20→EConsider the following statements about electric dipole and select the correct ones.
S1: Electric dipole moment vector →p is directed from the negative charge to the positive charge
S2: The electric field of a dipole potential falls off as 1r2 and not as 1r
S3: The electric field of a dipole at a point with position vector →r depends on |→r| as well as s angle between →rand→p
S4: In a uniform electric field, the electric dipole experience no net force but a torqueAS2,S3andS4BS2andS4CS2andS3Dall four
A charge Q located at a point →r is in equilibrium under the combined field of three charges q1,q2 and q3. If the charges q1 and q2 are located at point →r1 and →r2 respectively, find the direction of the force on Q due to q3 in terms of q1,(q2),→r1→r2, and →r.
View SolutionWhat is the direction of the force acting on a charged particle q, moving with a velocity →v a uniform magnetic field →B ?
View SolutionThere are two nonconducting spheres having uniform volume charge densities ρ and −ρ . Both spheres have equal radius R. The spheres are now laid down such that they overlap as shown in Fig.2.125. Take →d=O1−→O2.

The electric field →E in the overlapped region is
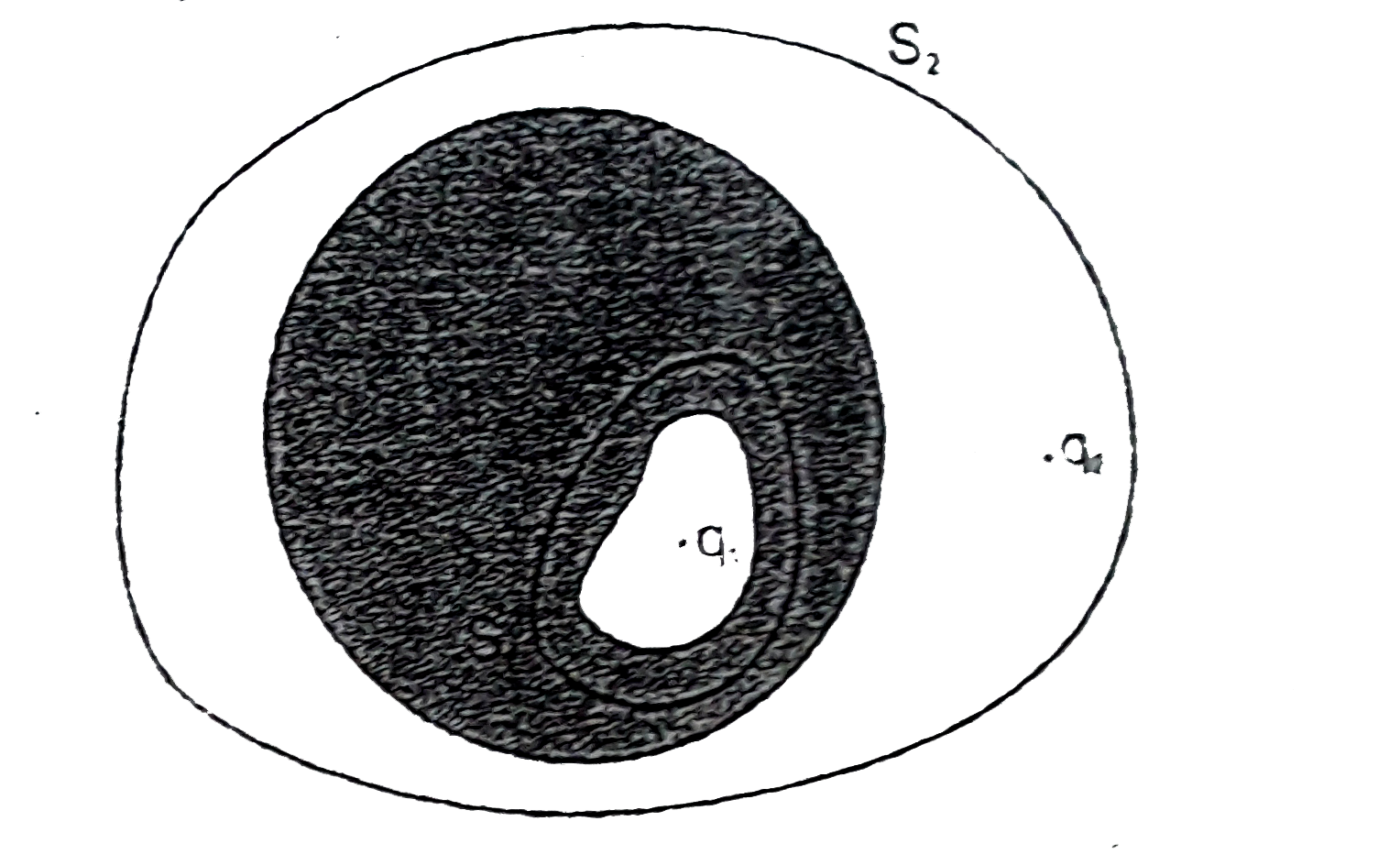
View SolutionFigure shows a conducting sphere with a cavity. A point charge q1 is placed inside cavity, and q2 is placed out side the sphere →Ein is electric field due to charge induced on surface of cavity. →Eout is electric field due to charge induced on outer surface of sphere and →Enet is net field at any point. Two closed gaussian surface S1 & S2 are also drawn in the figure.
View SolutionTwo particles A and B, move with constant velocities →v1 and →v2. At the initial moment their position vectors are →r1 and →r2 respectively. The condition for particle A and B for their collision is
View Solution
