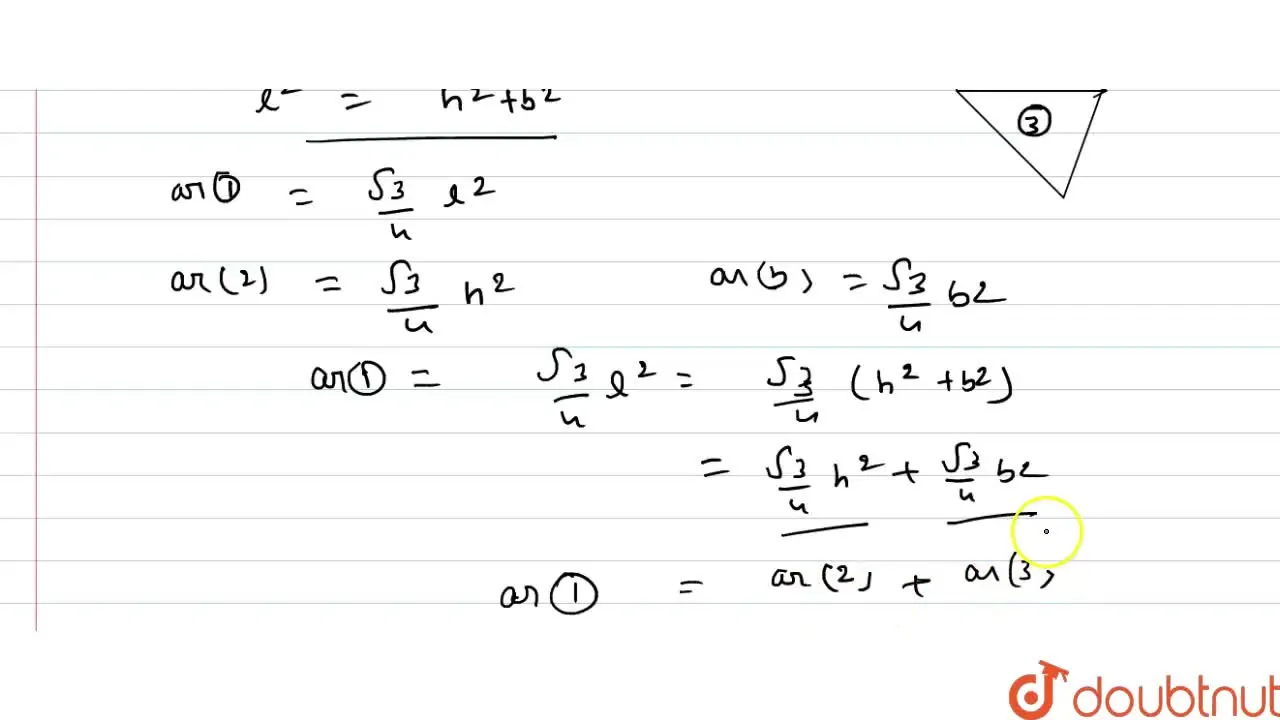सिद्ध कीजिए कि किसी समकोण त्रिभुज की दो भुजाओं पर बने समबाहु त्रिभुजों के क्षेत्रफलो का योग उसके विकर्ण पर बने समबाहु त्रिभुज के क्षेत्रफल के बराबर होता है |
माना कि, एक समकोण त्रिभुज ABC है जो B पर समकोण है | यहाँ ABD, BCE तथा ACF समबाहु त्रिभुज है | हमे सिद्ध करना है कि
(△ABD) का क्षेत्रफल +(△BCE) का क्षेत्रफल =(△ACF) का क्षेत्रफल
माना कि,
चूँकि ∠ABC=90∘ तब पाइथागोरस प्रमेय द्वारा,
AC2=AB2+BC2=x2+y2
⇒AC=√x2+y2
हम जानते है कि समबाहु त्रिभुज का क्षेत्रफल =√34(भुजा)2
इसलिए, (△ABD) का क्षेत्रफल =√34⋅x2=√3⋅x24
तथा (△BCE) का क्षेत्रफल =√34⋅y2=√3(4)2
अतः (△ACF) का क्षेत्रफल =√34(√x(2)+y2)2=√34(x2+y2)=√34x2+√34y2
=(△ABD) का क्षेत्रफल +(△BCE) का क्षेत्रफल
Related Playlists
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.19videos
त्रिभुज
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.217videos
त्रिभुज
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात एव असमिकाएँ EXERCISE - स्वमूल्यांकन परीक्षण35videos
त्रिकोणमितीय अनुपात एव असमिकाएँ
- BOOK - BALAJI PUBLICATIONCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - स्वमूल्यांकन परीक्षण29videos
दो चर वाले रैखिक समीकरण युग्म
Similar Questions
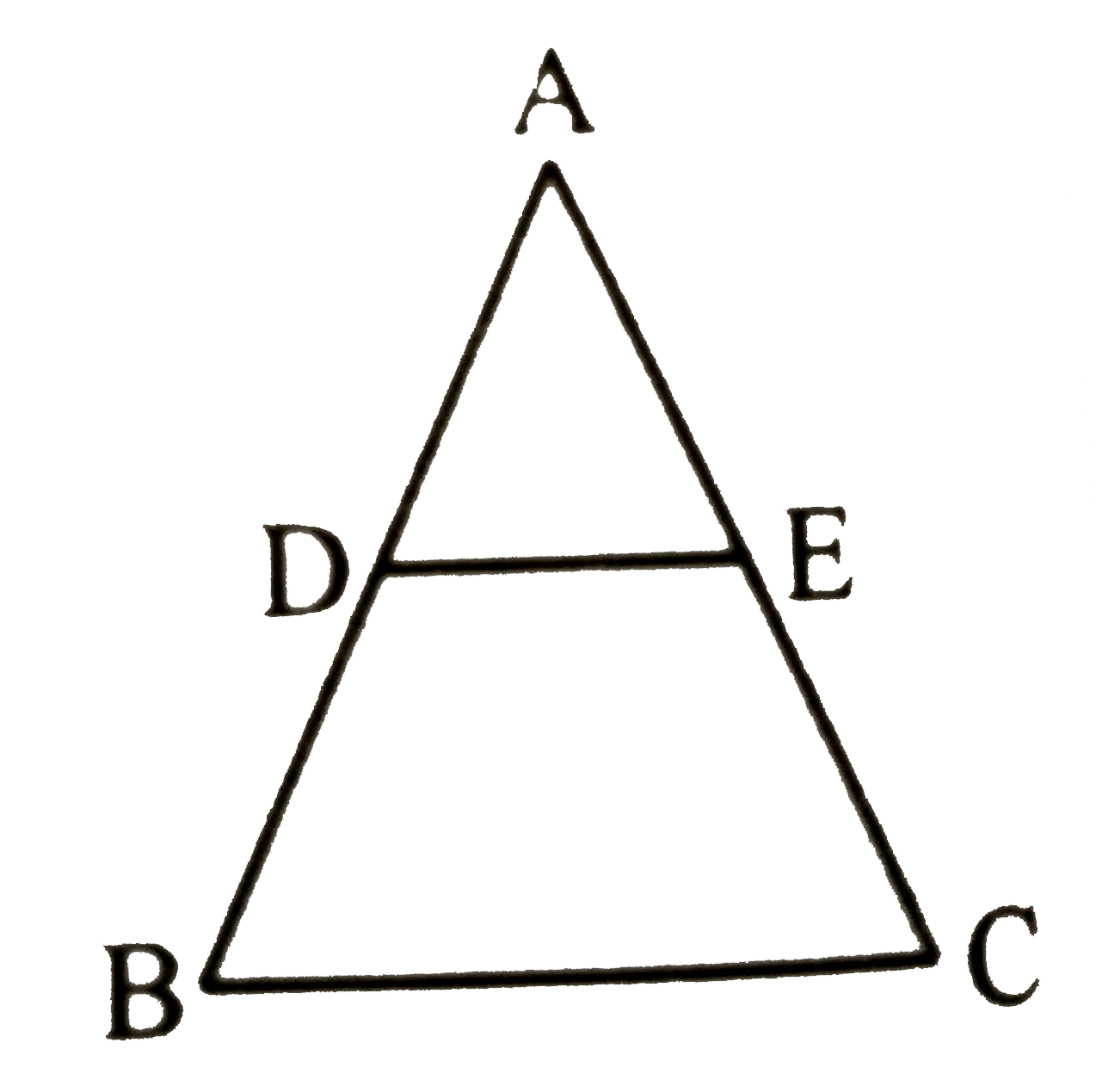
दी गई आकृति में DE∣∣BC यदि AD=2.5 सेमी, DB = 3 सेमी तथा AE = 3.75 सेमी है तो AC का मान ज्ञात कीजिए |
 07:55View Solution
07:55View Solutionदी गई आकृति में △ACB~△APQ है यदि BC=8 सेमी०, PQ=4 सेमी०, BA = 6.5 सेमी०, AP = 2.8 सेमी० है तो CA तथा AQ ज्ञात कीजिए |
 07:05View Solution
07:05View Solutionयदि cosθ=1√122, तब sinθ व tanθ के मान ज्ञात कीजिए.
04:17View Solutionकिसी भिन्न के अंश से यदि 1 घटाया जाये तो वह 13 तथा यदि हर में 8 जोड़ा जाये तो वह 14 हो जाती है। भिन्न ज्ञात कीजिए।
03:17View Solutionसिद्ध कीजिये की बिंदु (a,a),(-a,-a),(-a√3,a√3) एक समबाहु त्रिभुज के निर्देशांक है
05:20View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
04:32View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
02:30View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
49:09View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है। यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2) हो तो त्रिभुज की शेष दो भुजाओं के समीकरण ज्ञात कीजिए।
34:41View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
45:13View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 36∘ का कोण बनाती है| बहुभुज की भुजाओं की संख्या ज्ञात कीजिए |
03:46View Solutionएक त्रिभुज की दो भुजाओं की मापों का योग
01:02View SolutionRevision |दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु #!#एक त्रिभुज की दो भुजाओं की मापों का योग
44:35View Solutionदो या दो से आदिक सदिश राशियो को जोड़ना और घटाना #!#त्रिभुज के सदिश योग का नियम #!#त्रिभुज के सदिश योग का नियम पर आधारित प्रशन
43:44View SolutionThe diagonal of a square is equal to the side of an equilateral triangle. If the area of the square is 18 sqrt 3 sq.cm. What is the area (in cm^2 ) of the equilateral triangle? किसी वर्ग का विकर्ण एक समबाहु त्रिभुज की भुजा के बराबर है | यदि वर्ग का क्षेत्रफल 18 sqrt 3 वर्ग सेमी है, तो समबाहु त्रिभुज का क्षेत्रफल ( वर्ग सेमी में ) ज्ञात करें |
42:54View SolutionWhat is the area of an equilateral triangle of side 4 sqrt3 cm? 43 सेमी के समबाहु त्रिभुज का क्षेत्रफल कितना है?
45:16View Solution