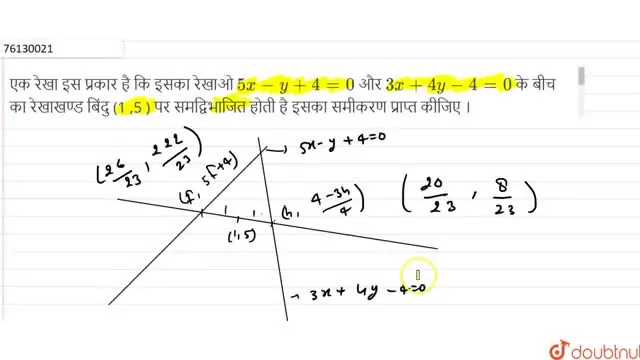
एक रेखा इस प्रकार है कि इसका रेखाओ 5x−y+4=0 और 3x+4y−4=0 के बीच का रेखाखण्ड बिंदु (1 ,5 ) पर समद्विभाजित होती है इसका समीकरण प्राप्त कीजिए ।
दी गई रेखाओ के समीकरण है :
5x−y+4=0
3x+4y−4=0
मान लीजिए एक रेखा उपरोक्त दोनों रेखाओ को क्रमश : (α1,β1) तथा (α2,β2) बिन्दुओ पर प्रतिच्छेद करती है ।
∴5α1−β1+4=0
या β1=5α1+4
और 3alpgha2+4β2−4=0
या β2=4−3a24
या β2=4−3a24
∵(α1,β1) तथा (α2,β2) बिन्दुओ वाली प्रतिछेदित रेखा का मध्य बिंदु (1 ,5 ) है ।
a1+a22=1 तथा β1+β22=5
या α1+α2=2तथा β1+β2=10
या α1+α2=2
तथा 5α1+4+4−3α24=10
या 2−α1+4−3α2=24
या 20α1−3α2=20
समीकरण (iii ) तथा (iv ) को हल पर
α1=2623 तथा c2=2023
अब β1=5×2623+c=22223
अंत : बिन्दुओ (1 ,5 ) तथा (2623,22223) से जाने वाली रेखा
y−5=22223−52623−1(x−1)
y−5=1073(x−1)
3y−15=107x−107
107x−3y−92=0
Related Playlists
- BOOK - MANOHAR RAYCHAPTER - सरल रेखाएँEXERCISE - प्रश्नावली 10(A)23videos
सरल रेखाएँ
- BOOK - MANOHAR RAYCHAPTER - सरल रेखाएँEXERCISE - प्रश्नावली 10(B)30videos
सरल रेखाएँ
- BOOK - MANOHAR RAYCHAPTER - सम्मिश्र संख्याएँ और द्विघातीय समीकरण EXERCISE - इंजीनियरिंग परीक्षाओं के प्रश्न2videos
सम्मिश्र संख्याएँ और द्विघातीय समीकरण
- BOOK - MANOHAR RAYCHAPTER - सांख्यिकीEXERCISE - विभिन्न इंजीनियरिंग परीक्षाओं के हल सहित प्रश्न6videos
सांख्यिकी
Similar Questions
निमिन्लिखित बिन्दुओ में से खींची जाने वाली रेखाओ की प्रत्येक प्रतिबंध के अनुसार प्रणवता ज्ञात कीजिए!
09:56View Solutionनिम्निलिखित बिन्दुओ से जाने वाली सरल रेखा का समीकरण ज्ञात कीजिए :
05:19View Solutionb के किस मान के लिए समीकरणों x2+bx−1=0,x2+x−b=0 का एक मूल उभयनिष्ठ होगा?
05:04View Solutionएक कक्षा के सभी विधार्थियों ने गणित में कम अंक प्राप्त किये । अध्यापक ने प्रत्येक विधार्थी को 10 रियायती अंक देने का निर्णय लिया । रियायती अंक देने के बाद भी निम्नलिखित में से कौन - सी सांख्यिकी माप नहीं बदलेगी ?
03:08View Solutionएक रेखा ऐसी है कि लाइनों 5x−y+4=0 तथा 3x+4y−4=0के बीच इसका खंड बिंदु (1,5) पर विभाजित है (1,5)। इसके समीकरण प्राप्त करें।
03:05View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
03:05View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
03:59View Solutionएक सरल रेखा द्वारा अक्षो के बीच काटे गये अन्तः खण्ड को बिंदु (7,9),3:1 के अनुपात में अन्तः विभाजित करता है रेखा का समीकरण ज्ञात कीजिए
04:37View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
03:24View Solutionबिंदु (4,−13) का रेखा 5x+y+6=0 पर प्रतिबिम्ब ज्ञात कीजिए
03:29View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए , जो रेखाओ x+y=3 तथा 2x+3y=7 के प्रतिच्छेद बिंदु को रेखाओ 2x+3y=8 तथा 3x−y=1 के प्रतिच्छेद बिंदु से मिलती है ।
04:46View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखा 7x−5y+14=0 के समान्तर है तथा रेखाओ 2x+3y+7=0 और 3x−4y−15=0 के प्रतिच्छेद बिंदु से होकर जाती है ।
03:29View Solutionदो बिंदु (1,3) और(0,4) इस प्रकार है की एक गतिमान बिंदु से बने त्रिभुज का क्षेत्रफल सदैव 25 वर्ग इकाई रहता है । उस बिंदु के बिन्दुपथ का समीकरण ज्ञात कीजिए
04:45View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
04:22View Solutionउस सरल रेखाओ के समीकरण ज्ञात कीजिए जो बिंदु (2,1)से जाती है तथा रेखाओ 4x−3y−5=0 और 5x−12y+3=0 से बराबर कोण पर झुकी है
05:09View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
04:21View Solution