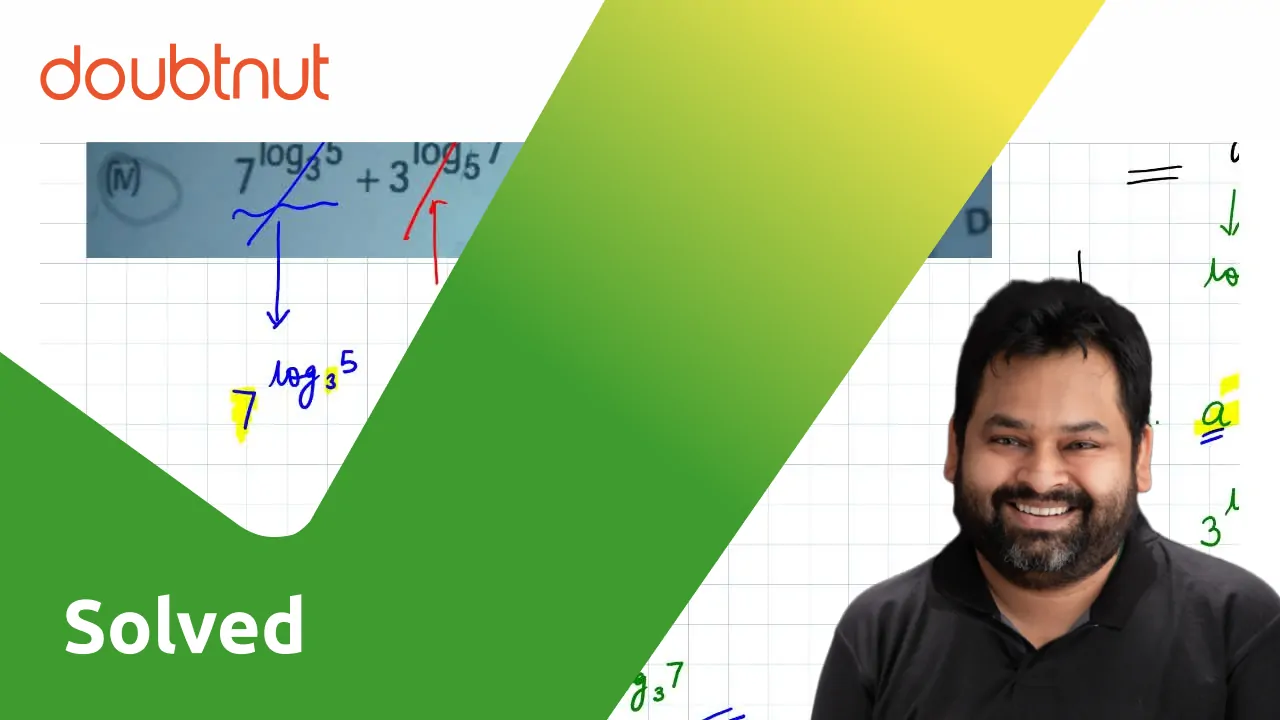
7log35+3log57−5log37−7log53
Video Solution
Text Solution
We know, logab=logxblogxa
So, 7log35=7log75log73
=(7log75)1log73 (As alogab=b)
=5(1log73) (As alogab=b)
=5log37 (As a1logbc=alogcb)
So,7log35=5log37->(1)
Similarly, we can show that,
3log57=7log53->(2)
So, using (1) and (2), we can write our expression as,
5log37+7log53−5log37−7log53=0
Was this answer helpful?426
Updated on:21/07/2023
Similar Questions
Find the value of
(i)(log105)(log1020)+(log102)2 (ii)3√51log75+1(−log100.1)
(iii)log0.75log2√√10.125 (iv)5log√52+9log37−8log25
(v)(149)1+log72+5−log1/57 (vi)7log35+3log57−5log37−7log53Text SolutionView SolutionCalculate 7logg35+3log57−5log37−7log53
02:02View SolutionCalculate :
log34×log45×log56×log67×log7302:13View Solutionlog_(3) 4 log_(4) 5 log_(5) 6 log_(6) 7 log_(7) 8 log_(8) 9 The value of
03:02View SolutionArrange log25,log0.55,log75,log35 in decreasing order.
09:25View SolutionFind the value of the following:
(i) log102+log105
(ii) log3(√11−√2)+log3(√11+√2)
(iii) log735−log7505:28View Solution∣∣ ∣ ∣∣5√log535√log535√log533−log1/34(0.1)log0.0147log73735∣∣ ∣ ∣∣ is equal to ____
04:20View SolutionIf x = log_(5) 3+ log_)(7)5 + log_(9) 7 Is, then the value of x will be
03:22View Solution