A circle is touching the side BC of a $△$ ABC at point P and touching AB and AC produced at Q and R respectively. Prove that $A Q = \frac{1}{2} (perimeter of △ A B C) .$

Text Solution

Verified by Experts

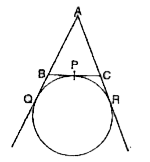
Given : triangle ABC and a circle which touches BC, AB and AC in P,Q and R respectively. Proof : Since the length of the two tangents drawn from an external point to a circle are equal therefore,

$A Q = A R ... (1)$
$B Q = B P ... (2)$
and $C P = C R ... (3)$
Now, perimeter of $△$ ABC=AB+BC+AC
$= A B + B P + P C + A C$
$= A B + B Q + C R + A C$ [from (2) and (3)]
$= A Q + A R = 2 A Q$ [from (1)]
$∴$ Perimeter of $△ A B C = 2 A Q$
$\Rightarrow A Q = \frac{1}{2} \times$ (perimeter of $△ A B C$ ) HenceProved.

Updated on:21/07/2023

A circle touches the side BC of a $Δ$ ABC at P and also touches AB and AC produced at Q and R, respectively. If the perimeter of $Δ$ ABC = 26.4 cm, then the length of AQ is:
A $8.8$ cm
B $13.2$ cm
C $15.4$ cm
D $17.6$ cm
In the figure shown here, a circle touches the side BC of a triangle ABC at P and AB and AC produced at Q and R respectively. What is AQ equal to ?

AOne-third of the perimeter of $Δ$ ABC.
BHalf of the perimeter of $Δ$ ABC.
CTwo-third of the perimeter of $Δ$ ABC
DThree-fourth of the perimeter of $Δ$ ABC