Question

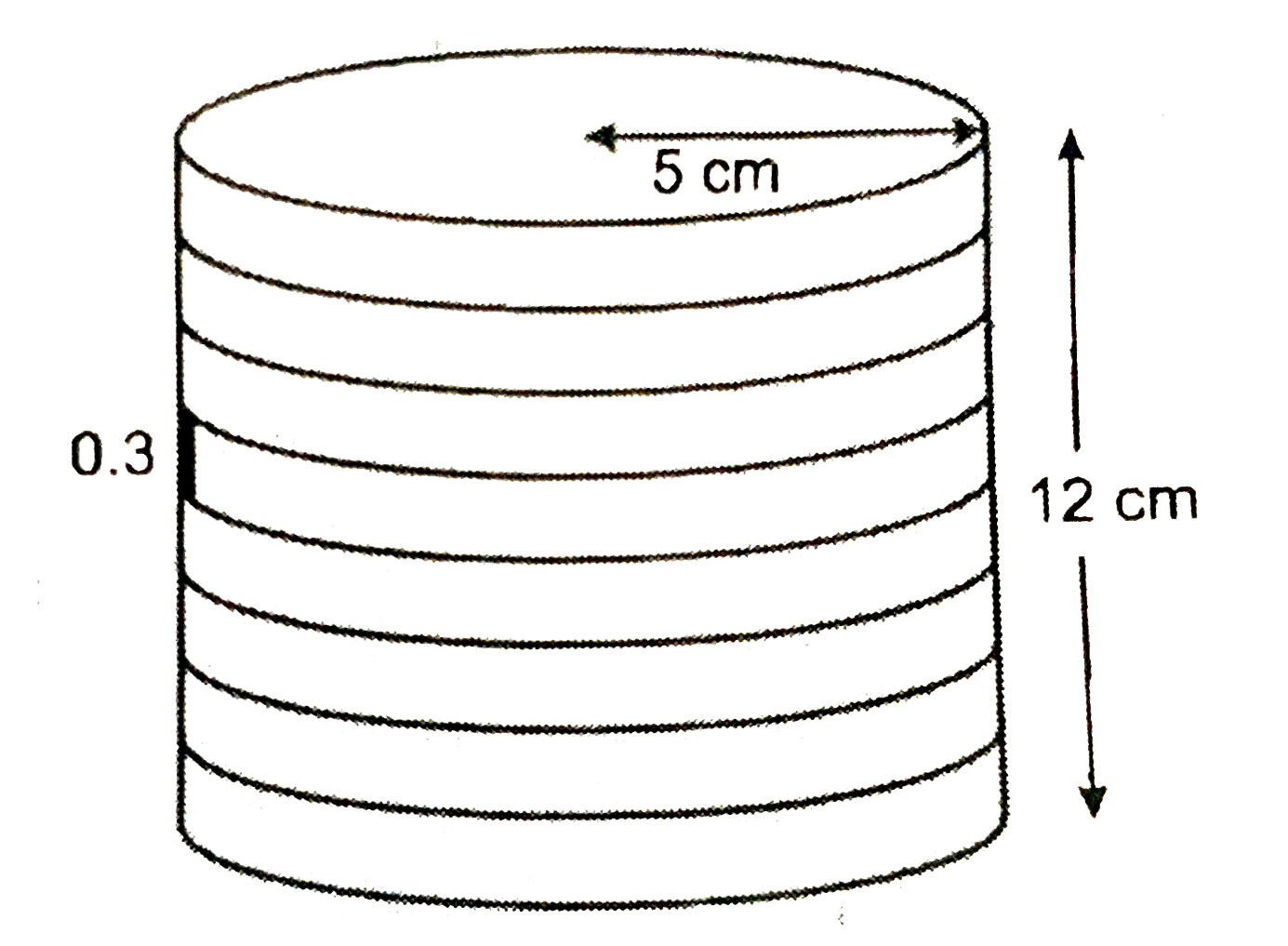
A copper wire, $3$ $mm$ in diameter, is wound about a cylinder whose length is $12$ $cm$, and diameter $10$ $cm$, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be $8.88$ $g$ $perc{m}^3$

Answer

19093 `cm^(3)`

Explanation

(i) Let the wire wounded around the cylinder completes n revolutions.
Diameter (width) of wire = 3m=0.3 cm
So whole height of cylinder =0.3 n cm
But whole height of cylinder =12 cm
0.3 `n=12 rarr n=(12)/(0.3)=(120)/(3)=40`
So 40 revolutions are completed to wound the wire completely on the cylinder
In I revolution length of wire = 2 `pi`r
In 40 revolutions length of wire =`40xx2pir`
`=80xx(22)/(7)xx5cm=1257.14 cm`
=12.57 m.(ii) Now radius of wire`=(0.3)/(2)=0.15 cm`
volume of wire =area of cross section`xx` length of wire
`=pi(0.15)^(2)xx1257.14=88.898 cm^(3)`
Mass of wire = volume `xx` density
=88.898`xx`8.88 g=789.41 g
Hence length of wire = 12.57 m
and mass of wire =789.41 g