A fair dice is rolled. Consider the following events: A={1,2,5},B={2,3} and C={2,3,4,5} Find (i) P(AB) and P(BC)
To solve the problem, we need to find the conditional probabilities P(A/B) and P(B/C) using the definitions of the events provided.
Given:
- Event A={1,2,5}
- Event B={2,3}
- Event C={2,3,4,5}
Step 1: Find P(A/B)
The formula for conditional probability is given by:
P(A/B)=P(A∩B)P(B)
Step 1.1: Find A∩B
The intersection A∩B consists of the elements that are common to both sets A and B.
- A∩B={2}
Step 1.2: Find n(A∩B)
The number of elements in A∩B:
- n(A∩B)=1
Step 1.3: Find n(B)
The number of elements in B:
- n(B)=2
Step 1.4: Calculate P(A/B)
Now substituting the values into the formula:
P(A/B)=n(A∩B)n(B)=12
Step 2: Find P(B/C)
Using the same formula for conditional probability:
P(B/C)=P(B∩C)P(C)
Step 2.1: Find B∩C
The intersection B∩C consists of the elements that are common to both sets B and C.
- B∩C={2,3}
Step 2.2: Find n(B∩C)
The number of elements in B∩C:
- n(B∩C)=2
Step 2.3: Find n(C)
The number of elements in C:
- n(C)=4
Step 2.4: Calculate P(B/C)
Now substituting the values into the formula:
P(B/C)=n(B∩C)n(C)=24=12
Final Answers:
1. P(A/B)=12
2. P(B/C)=12
---
- Event A={1,2,5}
- Event B={2,3}
- Event C={2,3,4,5}
1. P(A/B)=12
2. P(B/C)=12
Topper's Solved these Questions
Similar Questions
A fair dice is rolled. Consider the following events: A={1,2,5},B={2,3} and C={2,3,4,5} Find P(AB) and P(BC)
View SolutionA fair die is rolled. Consider events E={1,3,5}, F={2,3}and G={2,3,4,5}Find(i) P(E∣F)and P(F∣E) (ii) P(E∣G)and P(G∣E) (iii) P((E∪F)∣G)and P((E∩F)∣G)
View SolutionThe probabilities of outcomes of a random experiment are given below :
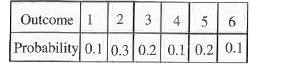
Let A = {2, 4, 6}, B = {1, 2, 3, 4} and C = {1, 2}. Then find P(A), P(B), P( C ), P(A∩B),P(B∩C) and P(C∩A).
View SolutionIf A and B are two events such that: P(A)= 1/3 , P(B)=1/4 and P(A∪B)=5/12 , find P(A/B) and P(B/A) .
View SolutionIf A and B are two events such that P(A)=13,P(B)=15 and P(A∪B)=1130, Find P(AB) and P(BA).
View SolutionIf A and B are events such that P(A)=12,P(B)=13andP(A∩B)=14, then find
(a) P(A/B)
(b) P(B/A)
View SolutionIf A and B are two events such that: P(A)=12 , P(B)=13 and P(A∩B)=14 , find (i) P(A/B) , (ii) P(B/A), (iii)P(A∪B).
View SolutionIf A and B are two events such
P(A)=12,P(B)=13andP(A∩B)=14,then find
(i) P(A/B). (ii) P(B/A).
(iii) P(A'/B). (iv) P(A'/B').
View SolutionIf A and B are two independent events and P(A)=0.2,P(B)=0.3, then find the values of the following:
(i) P (A and B) (ii) P (A and not B)
(iii) P (A or B) (iv) P (none of A and B)
View SolutionConsider the sets of A={1,4,3,2} and B={1,2,3,4} and C={1,5,3,7} and C={1,5,3,7} and insert the symbol ⊂or⊆ between each of the following pair or set.
(i) A__B
(ii) A__C
(iii) A__B
(iv) B__A
View Solution
