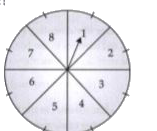
A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to all of the numbers 1, 2, 3, ...,12. What is the probability that it will point to (i) 10 (ii) an odd number (iii) a number which is multiple of 3?

Video Solution

Text Solution

Verified by Experts

n(S) = Total number of elementary events= 12.
(i) Favourable number of elementary events that points to 10 = 1
$∴ Required probability \frac{1}{12}$
(ii) Let A be the event "point of the arrow head towards an odd number"
$∴ n (A) = {1, 3, 5, 7, 9, 11} = 6$
$∴ P (A) = \frac{n (A)}{n (S)} = \frac{6}{12} = \frac{1}{2}$
(iii) Let E be the event "pointing towards a number which is a multiple of 3"
$∴ n (E) = {3, 6, 9, 12} = 4$
$∴ P (E) = \frac{n (A)}{n (S)} = \frac{4}{12} = \frac{1}{3}$

Updated on:21/07/2023

A game of chance consists of spinning an arrow, which comes to rest pointing at one of the numbers $1, 2, 3, 4, 5, 6, 7, 8$ and these are equally likely outcomes. Find the probability that the arrow will point at any factor of $8$ .
A $\frac{5}{8}$
B $\frac{7}{8}$
C $\frac{1}{8}$
D $\frac{3}{8}$
A number is selected from the numbers 1,2 …, 15. What is the probability that it is a multiple of 4?
A $\frac{7}{15}$
B $\frac{2}{5}$
C $\frac{1}{5}$
D $\frac{2}{15}$