A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4m from the mirror B, he can see the reflection of the top of the tree. How height is the tree ?Solution in Tamil
The correct Answer is:=10m
Step by step video, text & image solution for A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4m from the mirror B, he can see the reflection of the top of the tree. How height is the tree ? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - PREMIERS PUBLISHERSCHAPTER - GEOMETRYEXERCISE - SOLUTION TO THINKING CORNER
7 Videos
- GEOMETRYBOOK - PREMIERS PUBLISHERSCHAPTER - GEOMETRYEXERCISE - SOLUTION TO PROGRESS CHECK
21 Videos
- GEOMETRYBOOK - PREMIERS PUBLISHERSCHAPTER - GEOMETRYEXERCISE - SOLUTION TO EXERCISE 4.5
15 Videos
- CO-ORDINATE GEOMETRY BOOK - PREMIERS PUBLISHERSCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Other Important Objective
25 Videos
- MENSURATIONBOOK - PREMIERS PUBLISHERSCHAPTER - MENSURATIONEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
16 Videos
Similar Questions
Are square and a rhombus similar or congruent. Discuss.
View SolutionAll circles are …………. (congruent/similar).
View SolutionIf in triangles ABC and EDF, ABDE=BCFD then they will be similar, when
View SolutionThe area of the triangle formed by the points (0,0),(3,0) and (0,4) is :
View SolutionMatch the following:
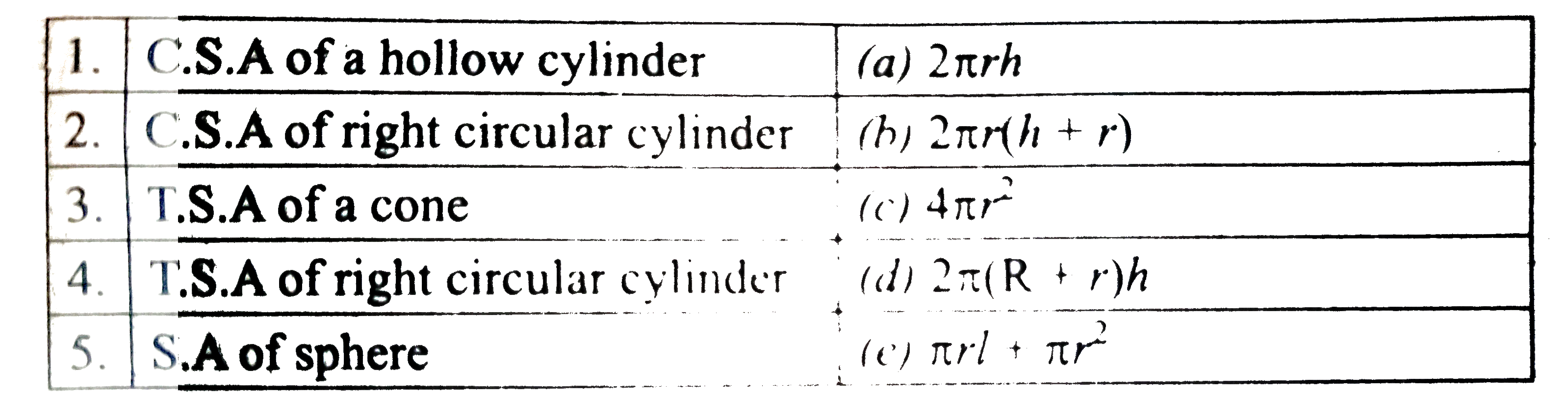
View SolutionA tree is broken at a height of 5m from the ground and its top touches the ground at a distance of 12m from the base of the tree. Find the original height of the tree
View SolutionA tree stands vertically on a hill side which makes an angle of 15owith the horizontal. From a point on the ground 35m down the hill from the base of the tree, the angle of elevation of the top of the tree is 60o. Find the height of the
View SolutionA tree stands vertically on a hill side which makes an angle of 150 with the horizontal. From a point on the ground 35 m down the hill from the base of three, the angle of elevation of the top of the tree is 600 . Find the height of the tree.
View Solutionएक पेड़ भूमि से 5m की ऊंचाई पर टूट जाता है और उसका ऊपरी सूरा भूमि को उसके आधार से 12m की दूरी पर छुता है। पेड़ की पूरी ऊंचाई ज्ञात कीजिए।
View SolutionA man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4m from the mirror B, he can see the reflection of the top of the tree. How height is the tree ?
View SolutionA tree stands vertically on the slant of the hills From a point A on the ground 35 meters. Down the hill from the base of the tree , the angle of elevation of the top of the tree is 60∘. If the angle of elevation of the foot of the tree A is 15∘, then the height of the tree.
View SolutionA tree of height 6 m breaks due to storm and the broken part bends at height 2 m from ground so that the top of the tree touches the ground, then angle made by top of tree with ground is
View SolutionA tree is broken by the wind. If the top of the tree struck the ground at an angle of 30∘ and at a distance of 30 m from the root, then the height of the tree is
View SolutionA tree stands vertically on a hill side which makes an angle of 15∘ with the horizontal. From a point on the ground 35m. Down the hill from the base of the tree, the angle of elevation of the top of the tree is 60∘. Find the height of the tree.
View Solutionएक वृक्ष का ऊपरी शीर्ष हवा से टूटकर भूमि से 30∘ का कोण बनाता है । वृक्ष की जड़ (Root) से उस बिंदु की दूरी 5 मी. है जहाँ शीर्ष भूमि को स्पर्श करता है । वृक्ष की ऊँचाई ज्ञात कीजिए।
View SolutionA tree stands vertically on a hill side which makes an angle of
15∘ with the horizontal. From a point on the ground 35m down the hill from the base of the tree, the angle of elevation of the top of the tree is
60∘ . Find the height of the tree.
View Solution
