A part of the locus of a point P, which is equidstant from two intersecting line as+by+c=0andpx+qy+r=0
(a−p)x+(b−q)y+(c−x)=0
ap+qby+cy=0
√a2+b2(px+qy+r)−√p2+q2(ax+by+a)
None of these
The correct Answer is:C
(i) Perpendicular distance of a point P(x1,y1) from the line, px+qy+r=0 is
|px1+qy1+r|√p2+q2,
(ii) Perpendicualr distance of the point (x1,y1) to the line ax+by+c=0 is
|ax1+qy1+c|√a2+b2,
Topper's Solved these Questions
- LOCUSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOCUSEXERCISE - Level 3
15 Videos
- LOCUSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOCUSEXERCISE - Level 1
15 Videos
- LINEAR EQUATIONS AND INEQUATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 3
10 Videos
- LOGARITHMSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOGARITHMSEXERCISE - Level 3 MCQ
15 Videos
Similar Questions
Knowledge Check
Shown below are the graphs of the lines y−2x=0,x+y=6andpx+qy=r
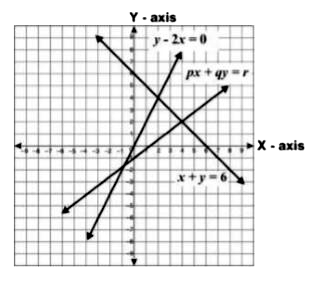
Which of these is the solution for the pair of equations x+y=6 and px+qy=rAx=2,y=4Bx=4, y=2Cx=3, y=2DWe cannot say for sure as the values of p and q are not known.
If the lines ax2 + 2xy + by2 = 0 meet the line px + qy = pq in points which are equidistant fromthe origin, prove that h(p? - q?) = pq(a - b).
View SolutionA line intersects x-axis at A(2,0) and y-axis at B(0,4). A variable lines PQ which is perpendicular to AB intersects x-axis at P and y-axis at Q. AQandBP intersect at R. The locus of R and the circle x2+y2−8y−4=0 (A) touch each other internally (B) touche the given circle externally (C) intersect in two distinct points (D) neither intersect nor touch each other
View SolutionStatement-l: If the diagonals of the quadrilateral formed by the lines px+gy+r=0,p'x+gy+r'=0,p'x+q'y+r'=0, are at right angles, then p2+q2=p2+q2. Statement-2: Diagonals of a rhombus are bisected and perpendicular to each other.
View SolutionLet a+b=2c. If ax+by+c=0 passes through A , 2bx−2ay+c=0 passes through B and C is point of intersection of lines then locus of point c is px2+qy2+rx+y=0. Find the value of p2+q2+r2
View SolutionFrom Figure, name All pairs of parallel lines. all pairs of intersecting lines. lines of whose point of intersection in P lines whose point of intersection in C lines whose point of intersection in R Collinear points.
View SolutionName the following from the figure given here.
(a) lines intersecting at point A.
(b) two parallel lines
(c ) four rays starting from point P.
(d) The point of intersection of lines l. and r.
View SolutionEquation of any circle passing through the point(s) of intersection of circle S=0 and line L=0 is S+kL=0. Let P(x1,y1) be a point outside the circle x2+y2=a2 and PAandPB be two tangents drawn to this circle from P touching the circle at AandB. On the basis of the above information : If P lies on the px+qy=r, then locus of circumcentre of ΔPAB is : (A) 2px+2qy=r (B) px+qy=r (C) px−qy=r (D) 2px−2py=r
View Solution
