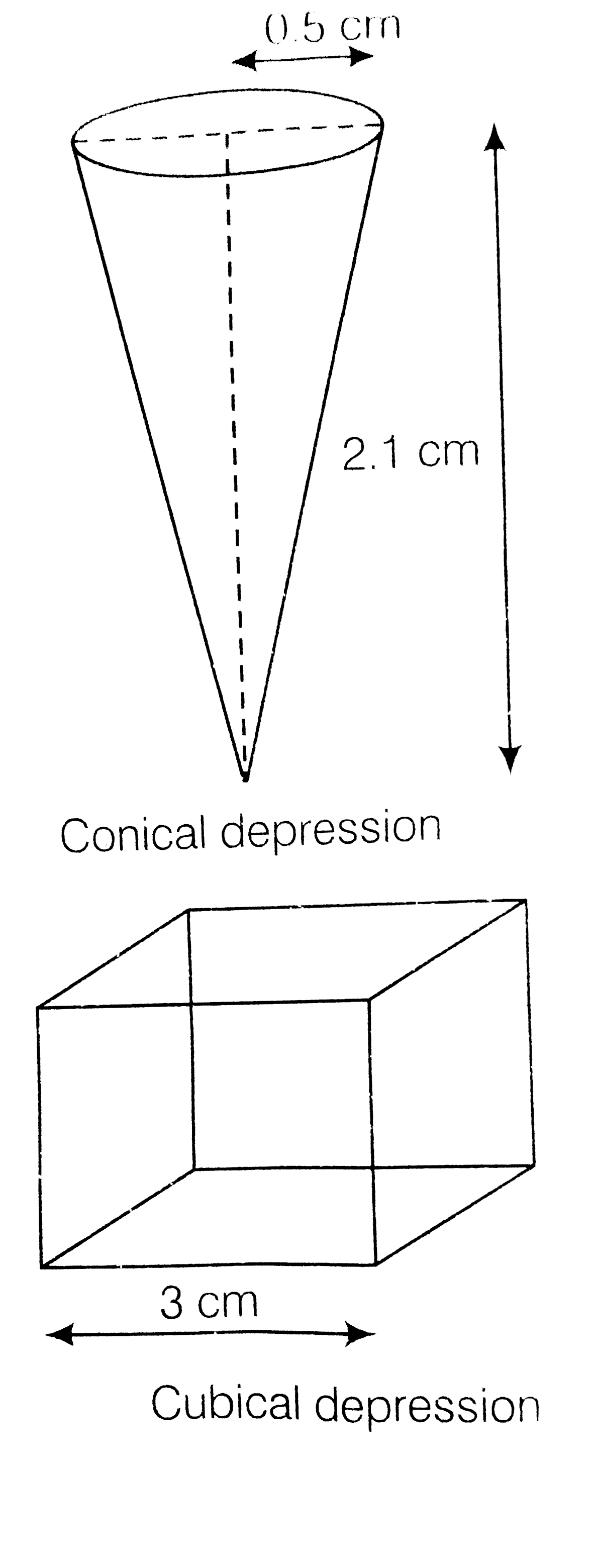
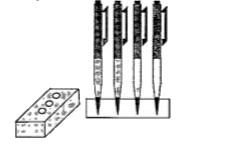
A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimension of the cuboid are 10 cm, 5 cm and 4 cm.The radius of the each of the conical depression is 0.5 cm and depth is 2.1 cm . The edge of the conical depression is 3 cm. Find the volume of the wood in the entire stand.
160cm2
150cm2
170.8cm2
None
The correct Answer is:C
Given that, length of cuboid pen stand (l) = 10 cm
Breadth of cuboid pen stand (b) = 4 cm
and height of cuboid pen stand (h) = 4 cm

∴ Volume of cuboid pen stand =l×b×h×=10×5×4=200cm3
Also, radius of conical depression (r) = 0.5 cm
and height (depth ) of a conical depression (h1) = 2.1 cm
∴ Volume of a conical depression =13πrh1
=13×227×0.5×0.5×2.1
=22×5×51000=2240=1120=0.55cm3
Also given
Edge of cubical depression (a) = 30
∴ Volume of cubical depression =(a)3=(3)3=27cm3
So, volume of 4 conical depressions
=4×Volume of a conical depression
=4×1120=115cm3
Hence , the volume of wood in the entire pen stand
= Volume of cuboid pen stand - Volume of 4 conical depression - Volume of cuboid depressions
=200−115−27=200−1465
=200−29.2=170.8cm3
So, the required volume of the wood in the entire stand is 170.8cm3.
(##ARH_NCERT_EXE_MATH_X_C12_S01_062_S03.png" width="80%">
Topper's Solved these Questions
Similar Questions
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15cm×10cm×3.5cm.The radius of each of the depression is 0.5 cm and the depht is 1.4 cm .Find the volume of the wood in the entire stand correct to 2 decimal places.
View SolutionA pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand
View Solution
Knowledge Check
The dimensions of a cuboid in cm are 10×9×5. The volume of the cuboid is
A225cm2B450cm2C675cm2D900cm2
Read the following text and answer the following questions on the basis of the same :
A pen stand made of wood is in the shape of a cuboid with 4 conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm
Find the diameter of each conical depression.
View SolutionRead the following text and answer the following questions on the basis of the same :
A pen stand made of wood is in the shape of a cuboid with 4 conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm
Find the volume of the cuboid
View SolutionThe dimensions of a cuboid are 5 cm, 3 cm and 2 cm. Draw three different isometric sketches of this cuboid.
View SolutionRead the following text and answer the following questions on the basis of the same :
A pen stand made of wood is in the shape of a cuboid with 4 conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm
Write the formula to find out volume of conical depression
View SolutionRead the following text and answer the following questions on the basis of the same :
A pen stand made of wood is in the shape of a cuboid with 4 conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm
Find the volume of wood in the entire stand
View SolutionThe dimensions of a cuboids are 8 cm, 2 cm, 1 cm. Then the total area of 4 walls is
View SolutionRead the following text and answer the following questions on the basis of the same :
A pen stand made of wood is in the shape of a cuboid with 4 conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm
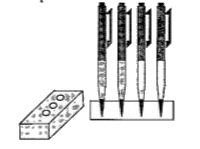
Find the volume of wood taken out to make four cavities.
View Solution
