A point moves in the straight line during the time t=0 to t=3 according to the law s=15t−2t2. The average velocity is
3 units
9 units
15 units
27 units
The correct Answer is:B
Step by step video, text & image solution for A point moves in the straight line during the time t=0 to t=3 according to the law s=15t-2t^2. The average velocity is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - EVALUATION TEST20videos
APPLICATIONS OF DERIVATIVES
- BOOK - TARGET PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - CRITICAL THINKING129videos
APPLICATIONS OF DERIVATIVES
- BOOK - TARGET PUBLICATIONCHAPTER - APPICATIONS OF DEFINITE INTEGRALEXERCISE - EVALUATION TEST18videos
APPICATIONS OF DEFINITE INTEGRAL
- BOOK - TARGET PUBLICATIONCHAPTER - BINOMIAL DISTRIBUTIONEXERCISE - EVALUTION TEST12videos
BINOMIAL DISTRIBUTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A body moves in a straight line according to the law s=t3−4t2−3t. What are the values of time and acceleration (time, acceleration), each time when velocity of the body is zero ?
A(3, -10)B(3, 10)C(2, -10)D(2, 10) - Question 2 - Select One
A body moves in a straight line along x-axis, its distance from the origin is given by the equation x=8t−3t2. The average velocity in the interval from t=0 to t=4 is
A2m/sB−16m/sC−4m/sD5m/s - Question 3 - Select One
Velocity-time graph of a particle moving in a straight line is shown in figure. In the time interval from t = 0 to t = 14 s, find:
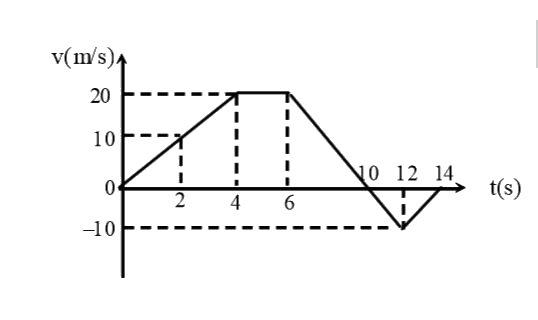
Q. average velocity andA(507)m/sB(257)m/sC(207)m/sD(157)m/s
A p article moves in a straight line such that its position in 't' time is s(t)=t2+3t−1 cm. find its velocity at t=4 sec.
View SolutionA particle moving in a straight line has its velocit varying with time according to relation v=t2−6t+8(m/s) where t is in seconds. The CORRECT statement(s) about motion of this particle is/are:-
View SolutionA particle moves along a straight line according to the law s=16−2t+3t3, where s metres is the distance of the particle from a fixed point at the end of t second. The acceleration of the particle at the end of 2s is
View SolutionA particle moves along a straight line according to the law s=16−2t+3t3 where s metres is the distance of the particle from a fixed point at the end of t sec the acceleration of the particle at the end of 2s is
View SolutionA particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View Solution