A point source of light is hung 30 feet directly above a straight horizontal path on which a man of 6 feet in height is walking. How fast is the man's shadow lengthening and how fast the tip of shadow is moving when he is walking away from the light at the rate of 100 ft/min.

Video Solution

Text Solution

Verified by Experts

Let A be the position of source of light.

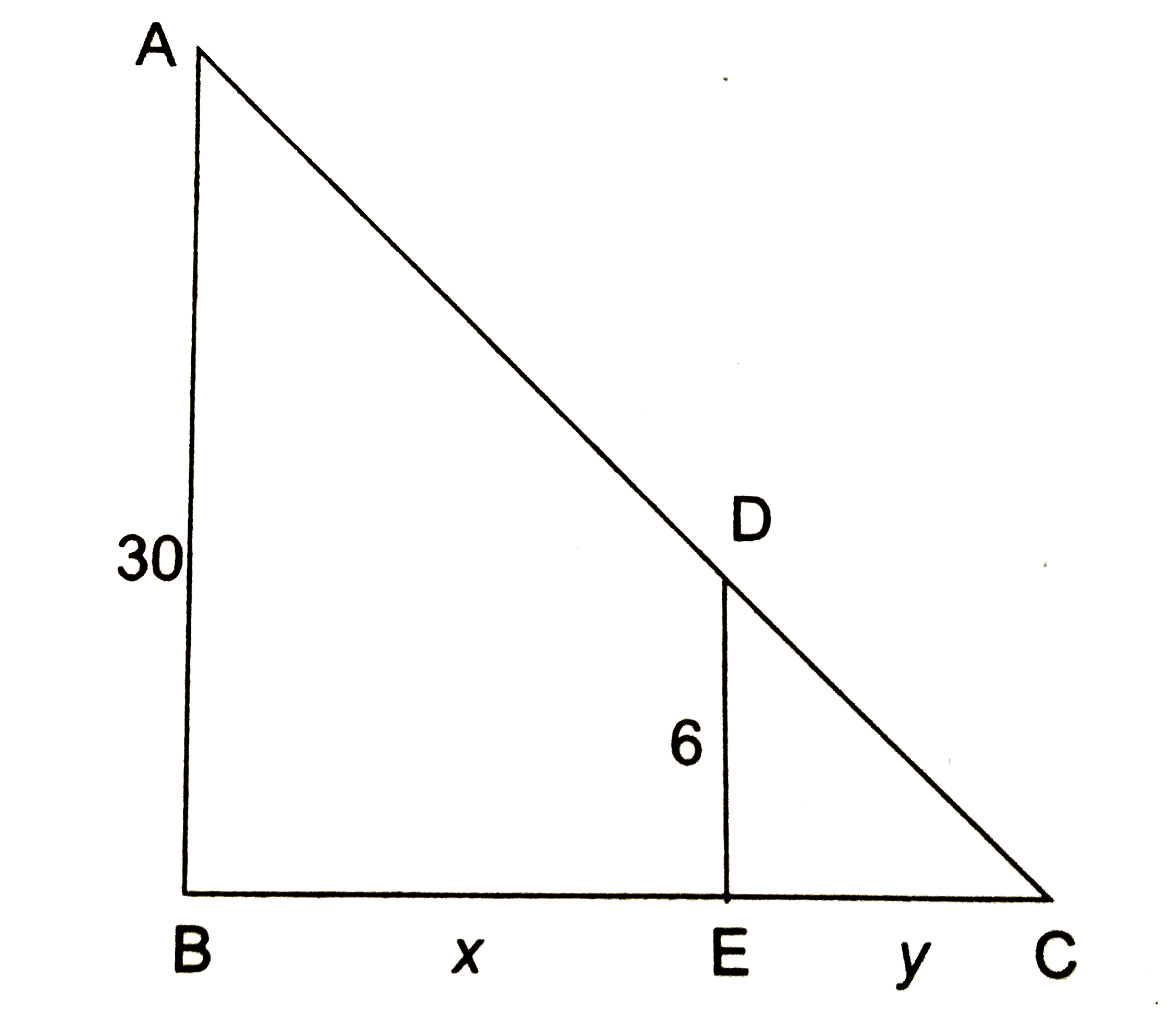
Let DE be the position of the man at a time t.
Let BE = x and EC = length of the shadow = u
Now, $\frac{d x}{d t} = 100 ft/min$ .
$∴ From figure, Δ B A C ~ Δ E D C$
$∴ \frac{B A}{E D} = \frac{B C}{E C}$
$\Rightarrow \frac{30}{6} = \frac{x + y}{y}$
$\Rightarrow 5 y = x + y$
$\Rightarrow y = \frac{x}{4}$
$\Rightarrow \frac{d y}{d t} = \frac{1}{4} \frac{d x}{d t}$
$= \frac{1}{4} \times 100 = 25$
$∴$ The shadow of the man is lengthening at the rate 25 ft/min.
The tip of shadow is at C.
Let $B C = a$
$∴ B E = x and E C = a - x$
$\frac{B A}{E D} = \frac{B C}{E C}$
$\Rightarrow \frac{30}{6} = \frac{a}{a - x}$
$\Rightarrow 5 a - 5 x = a$
$\Rightarrow 4 a = 5 x \Rightarrow a = \frac{5}{4} x$
$∴ \frac{d a}{d t} = \frac{5}{4} . \frac{d x}{d t} = \frac{5}{4} \times 100 = 125$
$∴ The tip of shadow is moving at the rate 125 ft/min.$

Updated on:21/07/2023