A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC.
or
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB+CD=BC+DA.
To prove that in a quadrilateral ABCD that circumscribes a circle, the relation AB+CD=AD+BC holds, we can follow these steps:
Step 1: Understand the properties of tangents
When a circle is inscribed in a quadrilateral, the tangents drawn from any external point to the circle are equal in length. This means that if we take any vertex of the quadrilateral, the lengths of the tangents from that vertex to the points where the circle touches the sides of the quadrilateral will be equal.
Step 2: Assign tangent lengths
Let:
- AP and AS be the lengths of the tangents from point A to the points where the circle touches sides AB and AD respectively.
- BP and BQ be the lengths of the tangents from point B to the points where the circle touches sides AB and BC respectively.
- CR and CQ be the lengths of the tangents from point C to the points where the circle touches sides BC and CD respectively.
- DR and DS be the lengths of the tangents from point D to the points where the circle touches sides AD and CD respectively.
From the properties of tangents, we have:
1. AP=AS
2. BP=BQ
3. CR=CQ
4. DR=DS
Step 3: Express the sides in terms of tangent lengths
Now, we can express the sides of the quadrilateral in terms of these tangent lengths:
- Side AB=AP+BP
- Side BC=BQ+CR
- Side CD=CQ+DR
- Side AD=AS+DS
Step 4: Write the equation
Now, we can sum the lengths of the sides:
- Left-hand side: AB+CD=(AP+BP)+(CQ+DR)
- Right-hand side: AD+BC=(AS+DS)+(BQ+CR)
Step 5: Substitute the equal lengths
Using the equal lengths from our earlier definitions:
- AP=AS
- BP=BQ
- CR=CQ
- DR=DS
We can substitute these into our equation:
- Left-hand side becomes: (AS+BQ)+(CQ+DR)
- Right-hand side becomes: (AS+DS)+(BQ+CR)
Step 6: Simplify the equation
Now we can simplify both sides:
- Left-hand side: AS+BQ+CQ+DR
- Right-hand side: AS+DS+BQ+CR
Since CQ=CR and DR=DS, both sides are equal.
Conclusion
Thus, we have shown that:
AB+CD=AD+BC
This completes the proof.
When a circle is inscribed in a quadrilateral, the tangents drawn from any external point to the circle are equal in length. This means that if we take any vertex of the quadrilateral, the lengths of the tangents from that vertex to the points where the circle touches the sides of the quadrilateral will be equal.
Let:
- AP and AS be the lengths of the tangents from point A to the points where the circle touches sides AB and AD respectively.
- BP and BQ be the lengths of the tangents from point B to the points where the circle touches sides AB and BC respectively.
- CR and CQ be the lengths of the tangents from point C to the points where the circle touches sides BC and CD respectively.
- DR and DS be the lengths of the tangents from point D to the points where the circle touches sides AD and CD respectively.
1. AP=AS
2. BP=BQ
3. CR=CQ
4. DR=DS
Now, we can express the sides of the quadrilateral in terms of these tangent lengths:
- Side AB=AP+BP
- Side BC=BQ+CR
- Side CD=CQ+DR
- Side AD=AS+DS
Now, we can sum the lengths of the sides:
- Left-hand side: AB+CD=(AP+BP)+(CQ+DR)
- Right-hand side: AD+BC=(AS+DS)+(BQ+CR)
Using the equal lengths from our earlier definitions:
- AP=AS
- BP=BQ
- CR=CQ
- DR=DS
- Left-hand side becomes: (AS+BQ)+(CQ+DR)
- Right-hand side becomes: (AS+DS)+(BQ+CR)
Now we can simplify both sides:
- Left-hand side: AS+BQ+CQ+DR
- Right-hand side: AS+DS+BQ+CR
Thus, we have shown that:
AB+CD=AD+BC
This completes the proof.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar11videos
CIRCLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise32videos
CIRCLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question5videos
ARITHMETIC PROGRESSION
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions10videos
CO-ORDINATE GEOMETRY
Similar Questions
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC
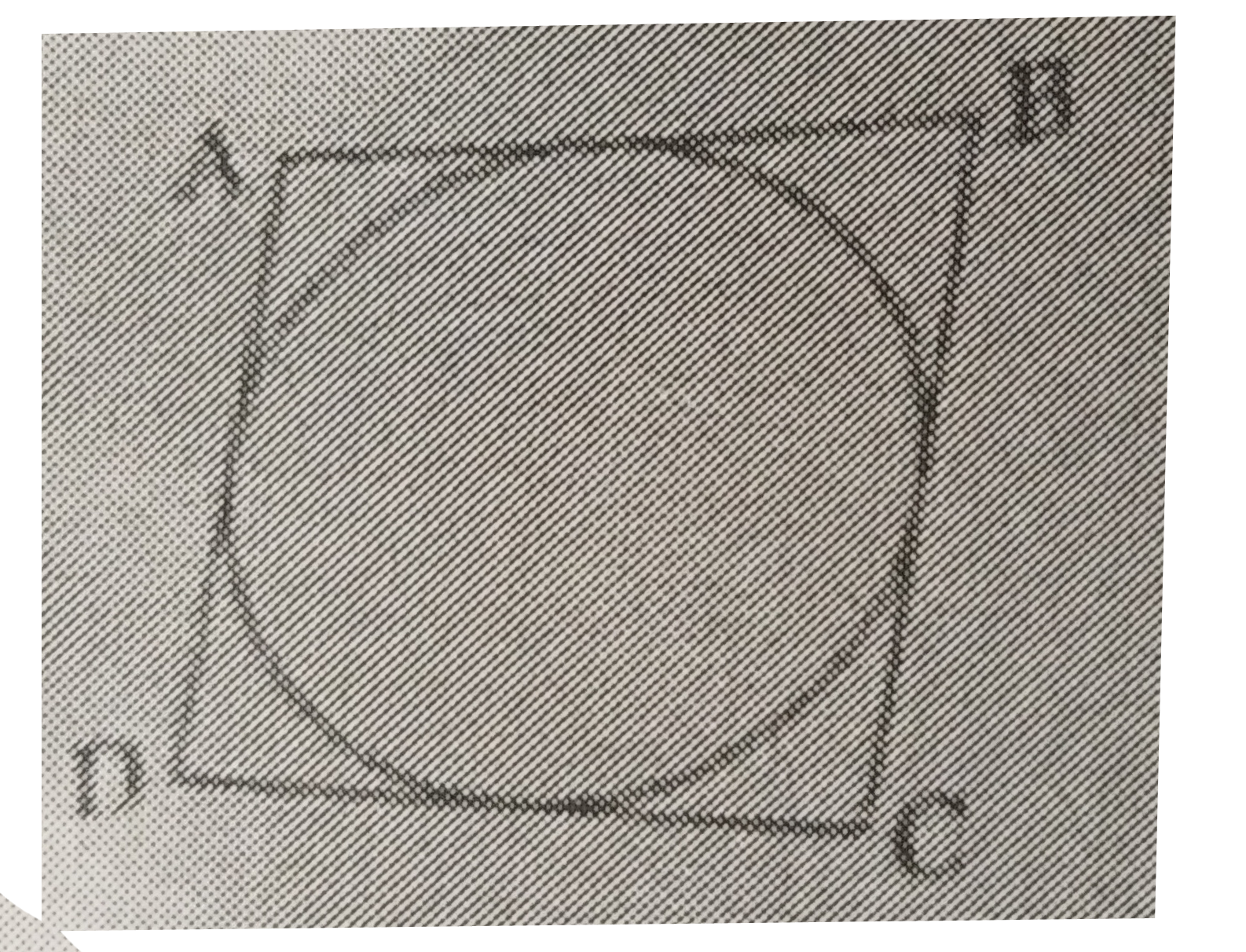
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD
 View Solution
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD
 View Solution
View SolutionIf the sides of a quadrilateral ABCD touch a circle prove that
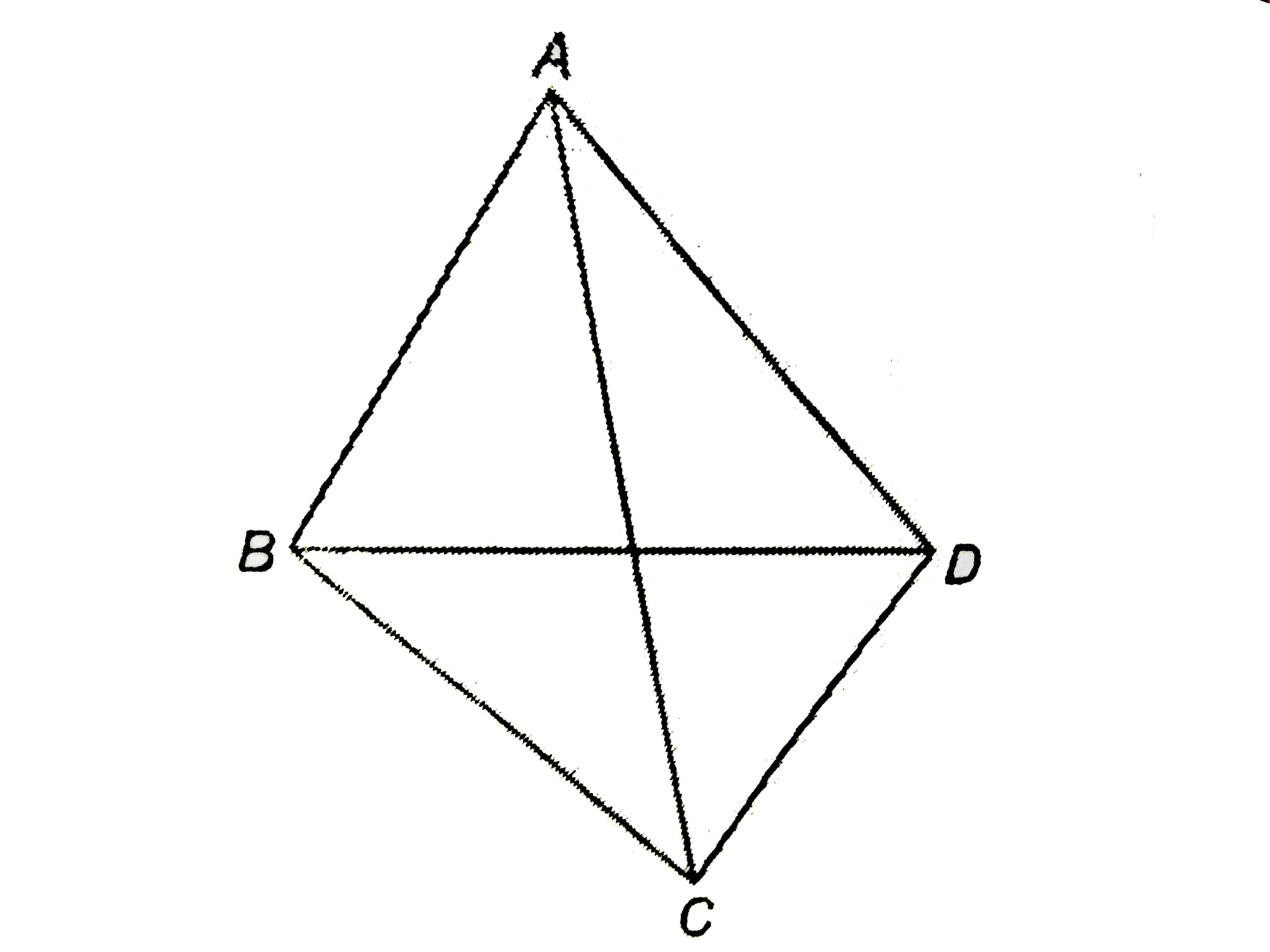
AB+CD=BC+AD.View SolutionThe given figure shows a quadrilateral ABCD. Prove that :
AB+BC+CD+DA>AC+BD
 View Solution
View SolutionIf a hexagon ABCDEF circumscribe a circle, prove that AB+CD+EF=BC+DE+FA
View SolutionIn a hexagon ABCDEF circumscribe a circle, prove that AB+CD+EF=BC+DE+FA.
View SolutionIf a hexagon ABCDEF circumscribe a circle, prove that AB+CD+EF=BC+DE+FA
View Solution
