A series whose terms are in Geometric progression is called ……. Solution in Tamil
The correct Answer is:Geometric series
Step by step video, text & image solution for A series whose terms are in Geometric progression is called ……. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NUMBERS AND SEQUENCESBOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - ACTIVITIES
9 Videos
- NUMBERS AND SEQUENCESBOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
23 Videos
- NUMBERS AND SEQUENCESBOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - THINKING CORNER
13 Videos
- MENSURATIONBOOK - PREMIERS PUBLISHERSCHAPTER - MENSURATIONEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
16 Videos
- RELATIONS AND FUNCTION BOOK - PREMIERS PUBLISHERSCHAPTER - RELATIONS AND FUNCTION EXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
25 Videos
Similar Questions
This activity helps you to find H.C.F. of two positive numbers. We first observe the following instructions.
Construct a rectangle whose length and breadth are the given numbers.
View SolutionThe quotient and remainder when 19 is divided by −3 are :
View SolutionWhen a positive integer is divided by 3
What are the possible remainders?
View SolutionMatch the following:
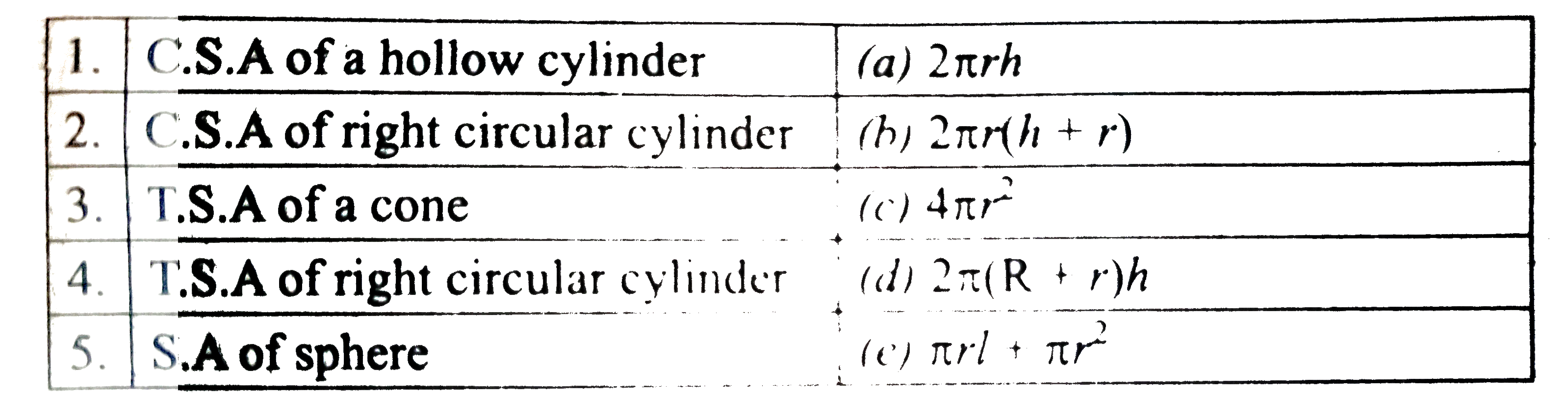
View SolutionIf n(A×B)=24andA={1,3,5,7}then n (B) is
View SolutionFor a series in geometric progression, the first term is a and the second term is 3a. The common ratio of the series is _______.
View SolutionIf every term of a series in geometric progression is multiplied by a real number, then the resulting series also will be in geometric progression. [True/False]
View SolutionThe reciprocals of all the terms of a series in geometric progression form a ________ progression.
View SolutionIf p, q, r be in arithmetic progression, then show that the pth, qth and rth terms of any geometric series will be in geometric progression.
View SolutionThe 4th term of a geometric progression is 23 and the seventh term is 1681. Find the geometric series.
View SolutionWrite the first 6 terms of the sequences whose nth terms are given below and classify them as arithmetic progression, geometric progression, arithmetico-geometric progression, harmonic progression and none of them.
12n+1
View SolutionWrite the first 6 terms of the sequences whose nth terms are given below and classify them as arithmetic progression, geometric progression, arithmetico-geometric progression, harmonic progression and none of them.
4(12)n
View SolutionWrite the first 6 terms of the sequences whose nth terms are given below and classify them as arithmetic progression, geometric progression, arithmetico-geometric progression, harmonic progression and none of them.
2n+33n+4
View SolutionSEQUENCE AND SERIES|GEOMETRIC PROGRESSION
View SolutionSEQUENCE AND SERIES#!#GEOMETRIC PROGRESSION
View Solution
