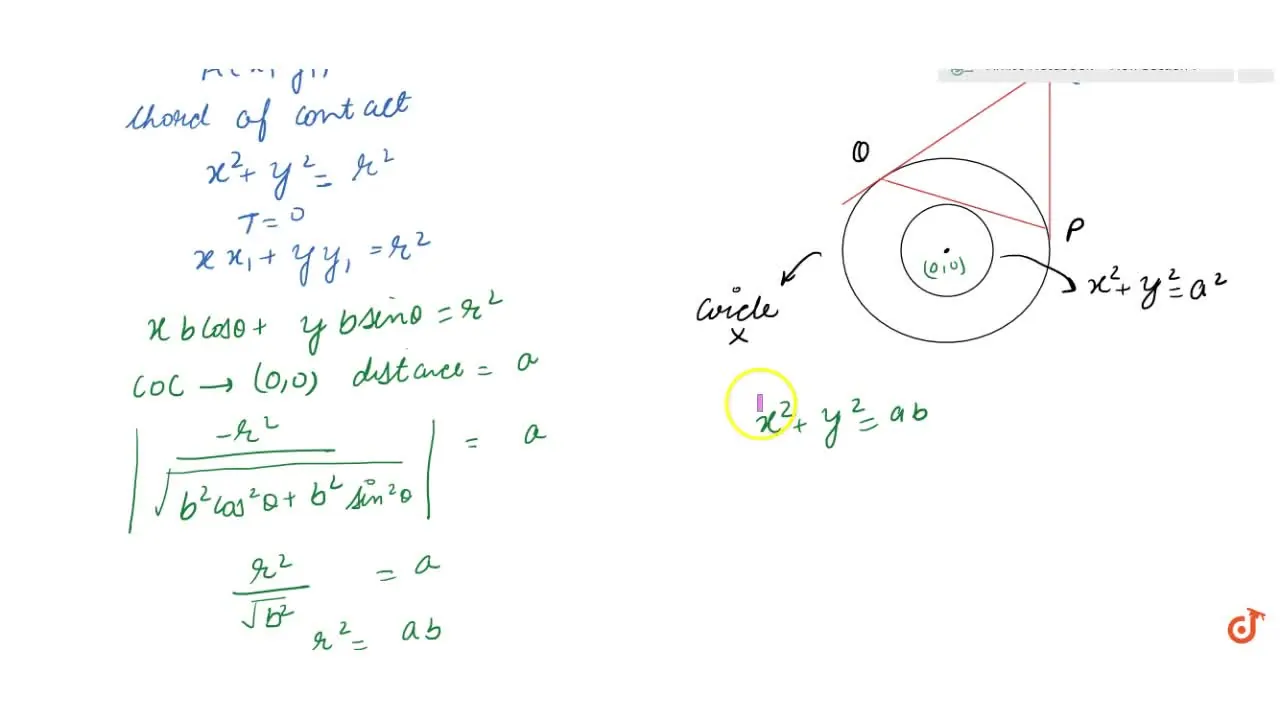
A tangent at a point on the circle x2+y2=a2 intersects a concentric circle C at two points PandQ . The tangents to the circle X at PandQ meet at a point on the circle x2+y2=b2. Then the equation of the circle is x2+y2=ab x2+y2=(a−b)2 x2+y2=(a+b)2 x2+y2=a2+b2
x2+y2=ab
x2+y2=(a−b)2
x2+y2=(a+b)2
x2+y2=a2=b2
The correct Answer is:1

Chord of contact of point A w.r.t x2+y2=r2 is
xbcosθ+ybsinθ=2 (1)
This must be a tangent to the circle x2+y2=a2. Therefore,
[r2√b2cos2θ+b2sin2θ]=a or r2=ab
Hence, the equation of circle is x2+y2=ab
Related Playlists
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)46videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.65videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank31videos
BINOMIAL THEORM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank32videos
CIRCLES
Similar Questions
A tangent at a point on the circle x2+y2=a2 intersects a concentric circle C at two points PandQ . The tangents to the circle X at PandQ meet at a point on the circle x2+y2=b2. Then the equation of the circle is x2+y2=ab x2+y2=(a−b)2 x2+y2=(a+b)2 x2+y2=a2+b2
View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x−2y=4. The radius of the circle is
View SolutionThe line 2x−y+1=0is tangent to the circle at the point (2,5) and the centre of the circles lies on x−2y=4 The radius of the circle is:
View SolutionThe line 2x - y + 1 = 0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x-2y = 4. The radius of the circle is :
View SolutionA tangent is drawn to the circle 2(x2+y2)−3x+4y=0 and it touches the circle at point A. If the tangent passes through the point P(2, 1),then PA=
View SolutionIf the line y=x+3 meets the circle x2+y2=a2 at A and B, then equation of the circle on AB as diameter is
View SolutionIf the line xcosα+ysinα=p and the circle x2+y2=a2 intersect at A and B then the equation of the circle on AB as diamerter is
View SolutionSlope of tangent to the circle (x−r)2+y2=r2 at the point(x.y) lying on the circle is
View SolutionIf tangent at (1, 2) to the circle C1:x2+y2=5 intersects the circle C2:x2+y2=9 at A and B and tangents at A and B to the second circle meet at point C, then the co- ordinates of C are given by
View SolutionThe tangent to the circle x2+y2=5 at the point (1,−2) also touches the circle x2+y2−8x+6y+20=0 at the point
View Solution