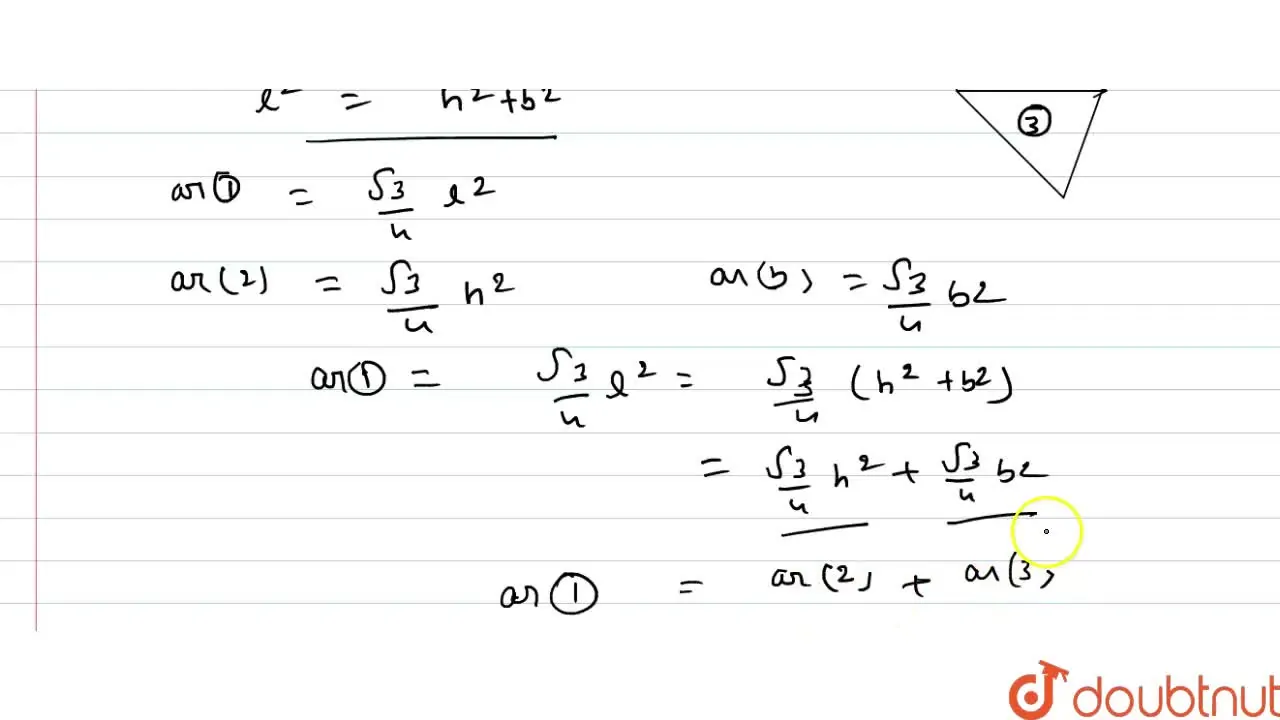एक समकोण त्रिभुज की एक भुजा पर समान कोण वाला त्रिभुज खींचा गया है | जिसमे लम्ब, आधार का दोगुना है | तो सिद्ध कीजिए कि कर्ण पर त्रिभुज का क्षेत्रफल वही है जो अन्य दो त्रिभुजों के क्षेत्रफलो का योग है |
माना AB = x इकाई, तब दिये अनुसार, BC = 2x इकाई
समकोण त्रिभुज ABC में, AC2=AB2+BC2
⇒AC2=x2+(2x)2=x2+4x2=5x2
चूँकि त्रिभुज समान कोणों वाले है इसलिए,
△ABD~△ACF
⇒(△ABD)का क्षेत्रफल(△ACF)का क्षेत्रफल=(AB)2(AC)2=x25x2=15
⇒(△ABD) का क्षेत्रफल =15(△ACF) का क्षेत्रफल ...(1)
यहाँ, △BCE~△ACF
⇒(△BCE)का क्षेत्रफल(△ACF)का क्षेत्रफल=(BC)2(AC)2=(2x)25x2=45
⇒(△BCE) का क्षेत्रफल =45(△ACF) का क्षेत्रफल ...(2)
समी० (1) तथा (2) को जोड़ने पर,
(△ABD) का क्षेत्रफल +(△BCE) का क्षेत्रफल
15(△ACF) का क्षेत्रफल +45(△ACF) का क्षेत्रफल +45(△ACF) का क्षेत्रफल
(1+45)(△ACF) का क्षेत्रफल
=(△ACF) का क्षेत्रफल
Related Playlists
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.19videos
त्रिभुज
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.217videos
त्रिभुज
- BOOK - BALAJI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात एव असमिकाएँ EXERCISE - स्वमूल्यांकन परीक्षण35videos
त्रिकोणमितीय अनुपात एव असमिकाएँ
- BOOK - BALAJI PUBLICATIONCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - स्वमूल्यांकन परीक्षण29videos
दो चर वाले रैखिक समीकरण युग्म
Similar Questions
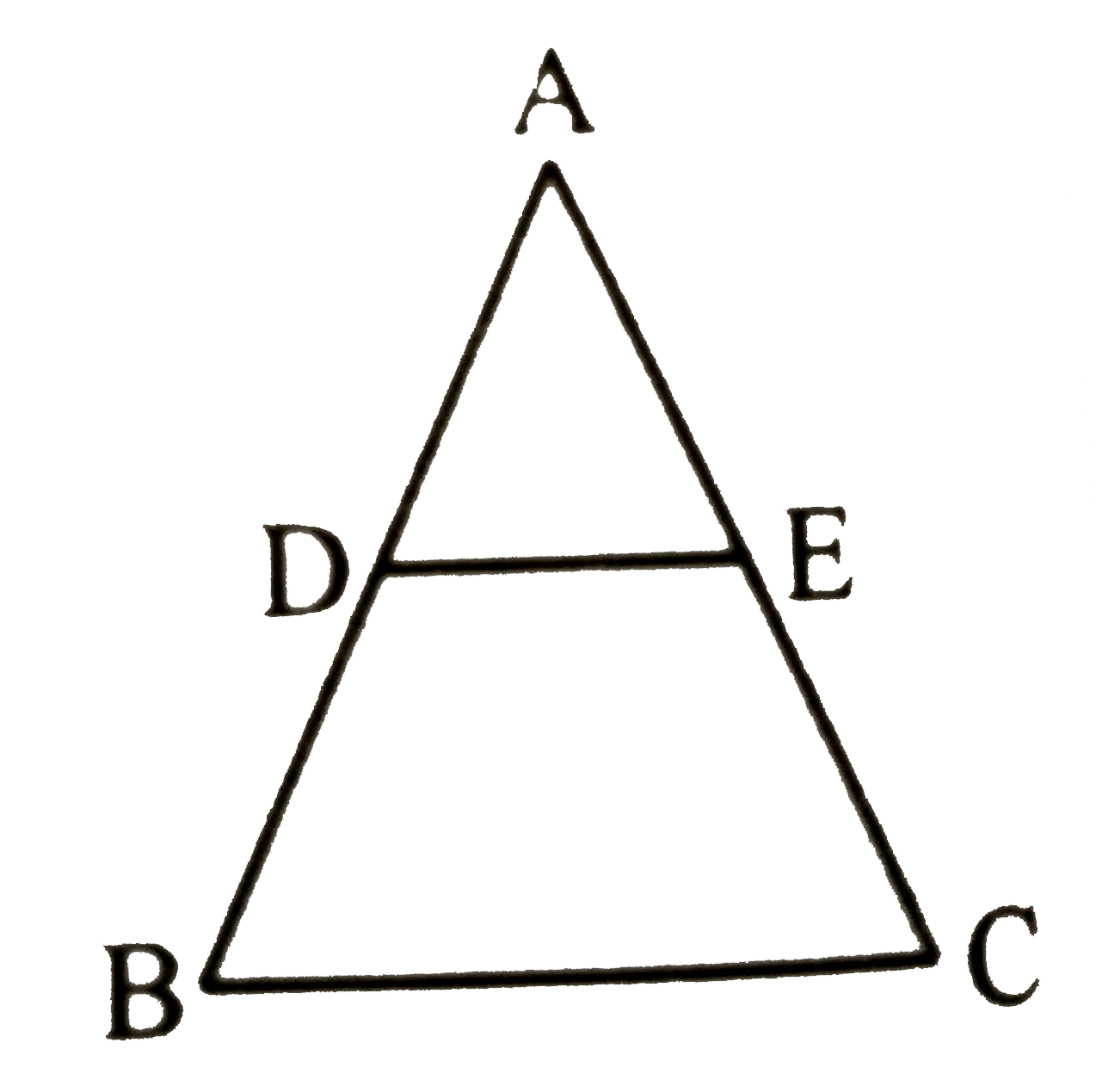
दी गई आकृति में DE∣∣BC यदि AD=2.5 सेमी, DB = 3 सेमी तथा AE = 3.75 सेमी है तो AC का मान ज्ञात कीजिए |
 05:04View Solution
05:04View Solutionदी गई आकृति में △ACB~△APQ है यदि BC=8 सेमी०, PQ=4 सेमी०, BA = 6.5 सेमी०, AP = 2.8 सेमी० है तो CA तथा AQ ज्ञात कीजिए |
 04:55View Solution
04:55View Solutionयदि cosθ=1√122, तब sinθ व tanθ के मान ज्ञात कीजिए.
07:05View Solutionकिसी भिन्न के अंश से यदि 1 घटाया जाये तो वह 13 तथा यदि हर में 8 जोड़ा जाये तो वह 14 हो जाती है। भिन्न ज्ञात कीजिए।
05:20View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
03:18View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है । यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2)है , तो त्रिभुज की शेष दो भुजाओ के समीकरण ज्ञात कीजिए ।
03:38View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
04:32View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है। यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2) हो तो त्रिभुज की शेष दो भुजाओं के समीकरण ज्ञात कीजिए।
03:50View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
05:59View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
49:09View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
39:49View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
01:53View Solutionमाना एक दीर्घवृत्त कि नाभियां S तथा S' है तथा इसके लघु अक्ष का कोई एक शीर्ष B है। यदि ΔS'BS एक समकोण त्रिभुज है जिसका समकोण B पर है तथा ΔS'BS का क्षेत्रफल 8 वर्ग इकाई है, तो दीर्घवृत्त की एक नाभिलम्ब जीवा की लम्बाई है
34:41View Solutionएक त्रिभुज की दो भुजाओं की मापों का योग
02:00View Solutionएक त्रिभुज का क्षेत्रफल
02:48View Solutionयदि दो समकोण त्रिभुजों में से एक त्रिभुज की एक भुजा और एक न्यूनकोण दूसरे त्रिभुज की एक भुजा और तदनुरूपी कोण के बराबर हो, तो दोनों त्रिभुज परस्पर क्या होंगे ?
02:37View Solution