A(6, 1), B(8, 2) and C(9, 4) are the vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ΔADE.
The correct Answer is:34 sq unit
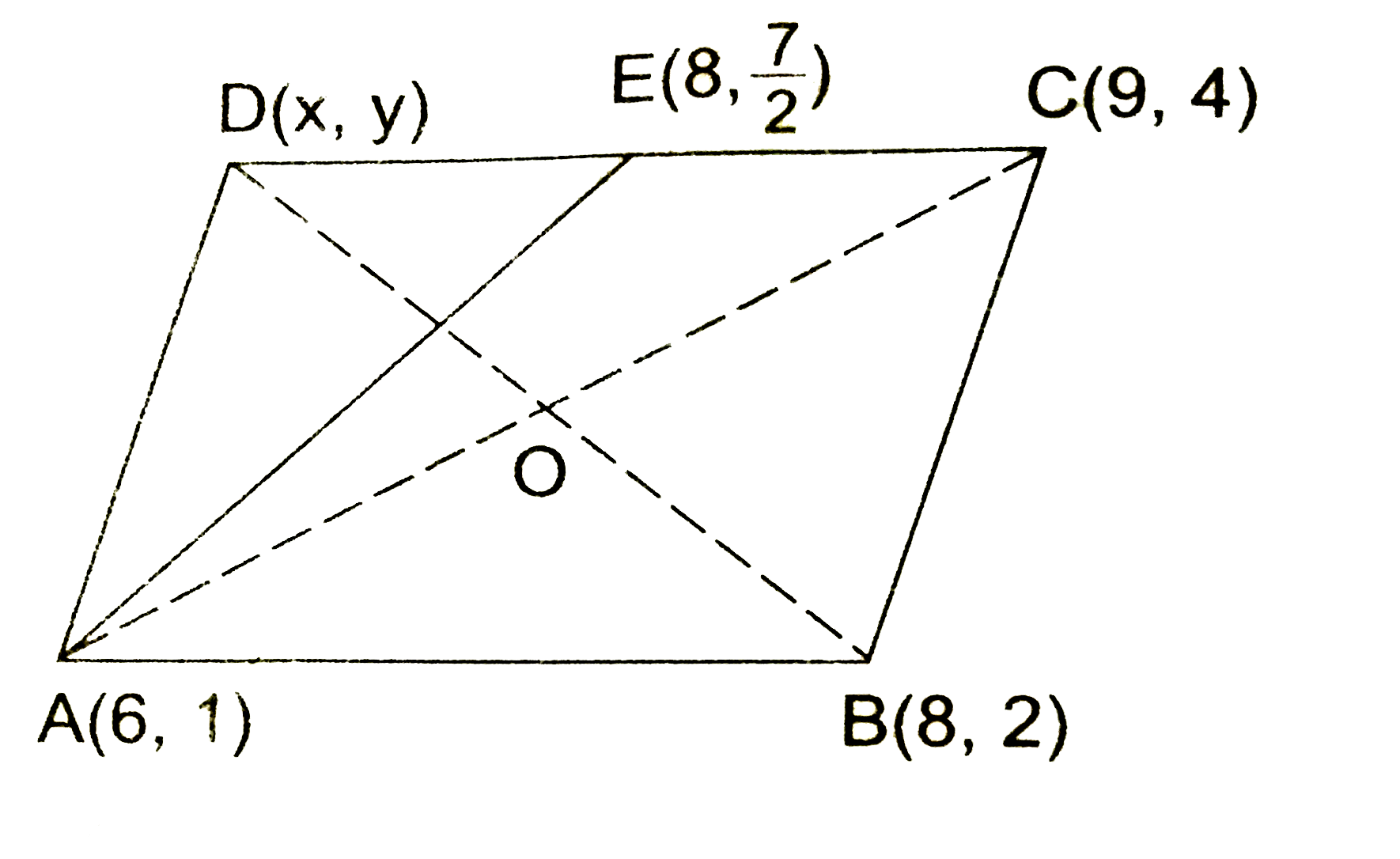
Let the fourth vertex be D(x, y).
Midpoint of AC is (6+92,4+12),i.e.,(152,52).
Midpoint of BD is (8+x2,2+y2)
∴8+x2=152and2+y2=52⇒x=7andy=3.
So, we get the point D(7, 3).
Midpoint of DC is E(7+92,3+42),i.e.,E(8,72)
Now, A(6, 1), D(7, 3) and E(8,72) are vertices of ΔABC. Now find its area.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 6D17videos
COORDINATE GEOMETRY
- BOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)34videos
COORDINATE GEOMETRY
- BOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 6B38videos
COORDINATE GEOMETRY
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself10videos
CONSTRUCTIONS
- BOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)25videos
HEIGHTS AND DISTANCES
Similar Questions
A(6,1),B(8,2)andC(9,4) are three vertices of parallelogram ABCD. If E is the mid-point of DC, then find the area of ΔADE.
View SolutionA(6,1) , B (8,2) and C (9,4) are three vertices of a parallelogram ABCD . If E is the mid - point of DC , then find the area of △ADE.
View SolutionIf A( 1,2) , B( 4,3) and C ( 0,0) are three vertices of parallelogram ABCD , find the coordinates of D.
View SolutionA(5, 4), B(-3, -2) and C(1,-8) are the vertices of a triangle ABC. Find the equation of median AD
View SolutionIf A(1, 2), B(4, 3) and C(6, 6) are the three vertices of a parallelogram ABCD , find the coordinates of fourth vertex D .
View SolutionThe points A(4,5,10),B(2,3,4)andC(1,2,−1) are three vertices of a parallelogram ABCD, then
View SolutionIf A(1, 2), B(4, 3) and C(6, 6) are the three vertices of a parallelogram ABCD, find the coordinates of the fourth vertex D.
View SolutionIf the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p.
View SolutionIf the points A(6, 1), B(8, 2), C(9, 4) and D(k, p) are the vertices of a parallelogram taken in order, then find the values of k and p .
View SolutionIf A(-1, 6), B(-3, -9) and C(5, -8) are the vertices of a △ABC, find the equations of its medians.
View Solution


