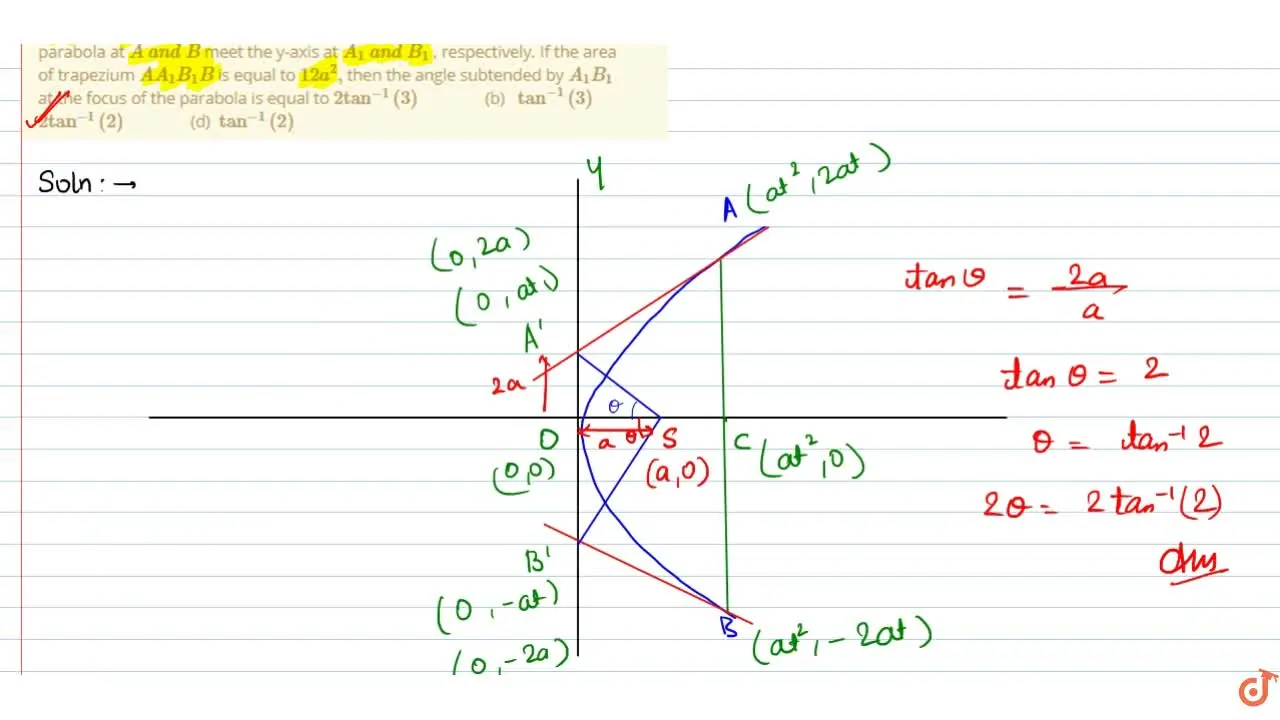
AB is a double ordinate of the parabola y2=4ax. Tangents drawn to the parabola at AandB meet the y-axis at A1andB1 , respectively. If the area of trapezium ∀1B1B is equal to 12a2, then the angle subtended by A1B1 at the focus of the parabola is equal to 2tan−1(3) (b) tan−1(3) 2tan−1(2) (d) tan−1(2)
2tan−1 (3)
tan−1 (3)
2tan−1 (2)
tan−1 (2)
The correct Answer is:C
(3) Let A≡(at21,2at1)
andB≡(at21,−2at1)
The equation of tangents at A and B are, respectively,
t1y=x+at21
and−t1y=x+at21
These tangents meet the y-axis, respectively, at
A1≡(0,at1)
andB1≡(0,−at1)
Area of trapezium
AA1B1B=12(AB+A1B1)×OC
∴ 24a2=12(4at1+2at1)(at21)
or t31=8ort1=2
∴ A1≡(0,2a)
If ∠OSA1=θ,then
tanθ=2aa=2
Thus, the middle required angle is 2tan−12.

Related Playlists
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Multiple)26videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Comprehension)41videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise 5.79videos
PARABOLA
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank19videos
PERMUTATION AND COMBINATION
Similar Questions
Tangent and normal are drawn at the point P≡(16,16) of the parabola y2=16x which cut the axis of the parabola at the points AandB , rerspectively. If the center of the circle through P,A,andB is C , then the angle between PC and the axis of x is (a)tan−1(12) (b) tan−12 (c)tan−1(34) (d) tan−1(43)
View SolutionFind the angle between the tangents drawn from the origin to the parabolas y2=4a(x−a) (a) 90∘ (b) 30∘ (c) tan−1(12) (d) 45∘
View SolutionA vertical pole subtends an angle tan−1(12) at apoint P on the ground. The angle subtended by the upper half of the pole at the point P is (A) tan−1(14) (B) tan−1(29) (C) tan−1(18) (D) tan−1(23)
View SolutionDouble ordinate AB of the parabola y2=4ax subtends an angle π2 at the focus of the parabola. Then the tangents drawn to the parabola at AandB will intersect at (−4a,0) (b) (−2a,0) (−3a,0) (d) none of these
View SolutionWhat is the angle between vector A and the resultant of vector(A+B) and vector(A-B)? (2) tan (B) 1(A-B ) ) (3) tan-1 (4) tan-1 (4) tan-1 -B
View SolutionIf the line x+y−1=0 is a tangent to a parabola with focus (1,2) at A and intersect the directrix at B and tangebt at vertex at C respectively, then AC.BC is equal to
View SolutionIf tanA=12 and tanB=13, then tan(A+B) is equal to
View SolutionIf tanA=12 and tanB=13, then tan(2A+B) is
View SolutionTwo mutually perpendicular tangents of the parabola y2=4ax meet the axis at P1andP2 . If S is the focus of the parabola, then 1SP1 is equal to 4a (b) 21 (c) 1a (d) 14a
View SolutionParabola y2=x+1 cuts the Y-axis in A and B. The sum of slopes of tangents to the parabola at A and B is
View Solution