Question

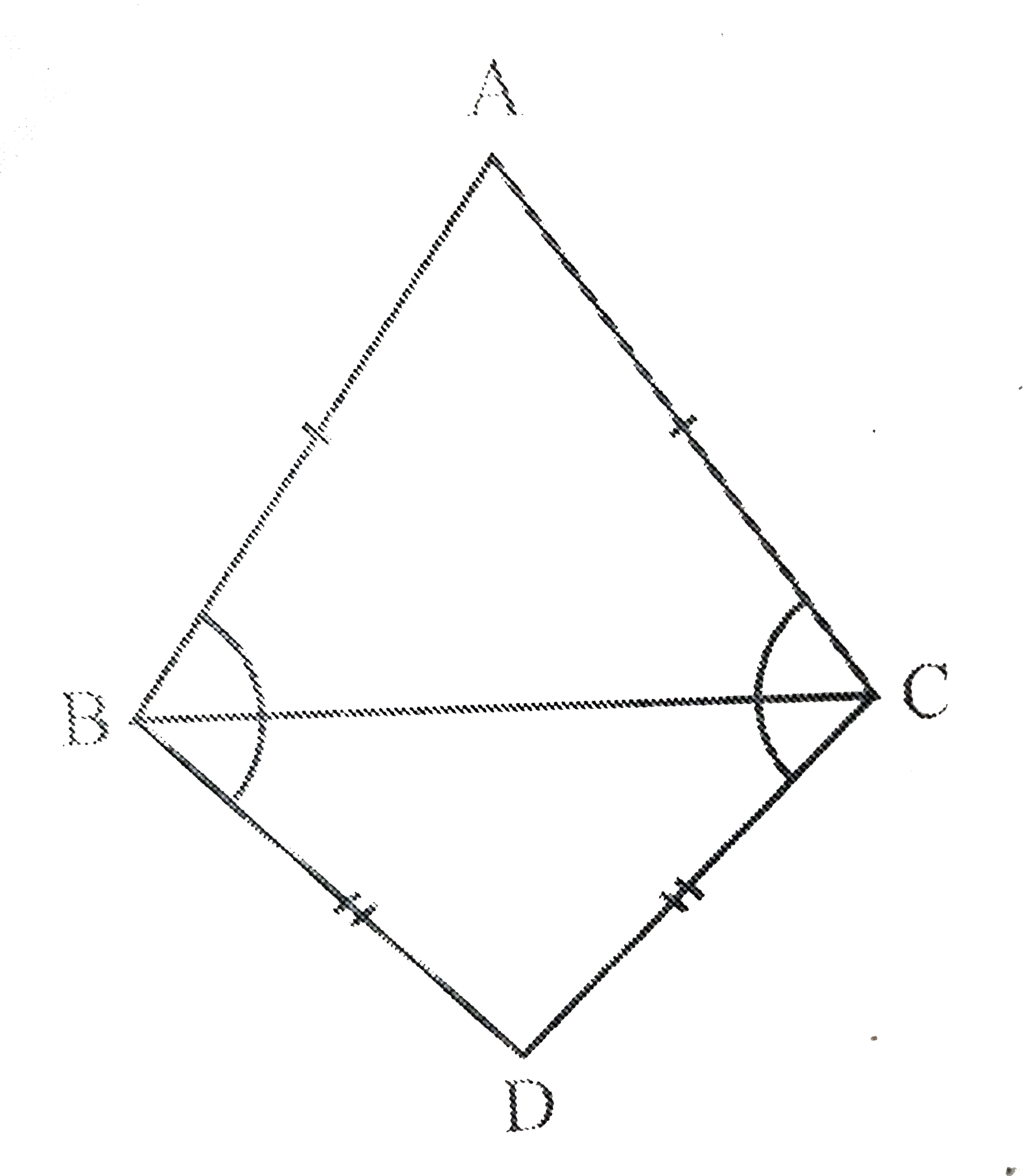
ABC and DBC are two triangle on the same base BC such that A and D lie on the opposite sides of BC,AB=AC and DB =DC ,Show that AD is the perpedicular bisector of BC.

Explanation

To show that line AD is the perpendicular bisector of line segment BC in triangles ABC and DBC, we can follow these steps:

1. Identify Given Information:
- We have two triangles, ABC and DBC, sharing the same base BC.
- Points A and D lie on opposite sides of line BC.
- It is given that AB = AC and DB = DC.

2. Establish Congruence of Triangles:
- In triangles ABD and ACD, we know:
- AB = AC (given)
- BD = CD (given)
- AD is common to both triangles.
- Therefore, by the Side-Side-Side (SSS) congruence criterion, we can conclude that triangle ABD is congruent to triangle ACD.

3. Use CPCTC:
- Since triangles ABD and ACD are congruent, by the Corresponding Parts of Congruent Triangles are Congruent (CPCTC), we have:
- ∠BAD = ∠CAD.

4. Consider Smaller Triangles:
- Now, consider triangles BAO and CAO, where O is the foot of the perpendicular from A to line BC.
- We know:
- AB = AC (given)
- ∠BAO = ∠CAO (because ∠BAD = ∠CAD).
- AO is common to both triangles.
- Therefore, by the Side-Angle-Side (SAS) congruence criterion, triangles BAO and CAO are congruent.

5. Apply CPCTC Again:
- From the congruence of triangles BAO and CAO, we have:
- ∠AOB = ∠AOC.

6. Linear Pair of Angles:
- Angles AOB and AOC are a linear pair (they lie on the same line BC).
- Thus, we have:
- ∠AOB + ∠AOC = 180°.

7. Set Up the Equation:
- Since ∠AOB = ∠AOC, we can write:
- ∠AOB + ∠AOB = 180°,
- 2∠AOB = 180°.

8. Solve for ∠AOB:
- Dividing both sides by 2 gives:
- ∠AOB = 90°.

9. Conclusion:
- Since ∠AOB = 90°, this means that line AD is perpendicular to line BC.
- Additionally, since O is the midpoint of BC (as shown by the congruence of triangles), AD is also the bisector of BC.
- Therefore, AD is the perpendicular bisector of BC.