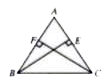
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that(i) ΔABE≅ΔACF(ii) AB = AC, i.e., ABC is an isosceles triangle
The correct Answer is:AC
Step by step video solution for ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that(i) DeltaA B E~=DeltaA C F(ii) A B\ =\ A C, i.e., ABC is an isosceles triangle by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.3
5 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.4
6 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - SUMS TO ENRICH REMEMBER
9 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
Knowledge Check
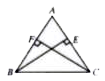
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
A∠B=∠CB∠BAE=∠FACC∠AFC=∠AEBDBE = CF
ABC is a triangle in which altitude BE and CF drawn on AC and AB respectively are equal. Prove that ΔBEC≅ΔCFB
View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.

View SolutionIn quadrilateral ACBD, AC = ADand AB bisects ∠A(see Fig. 7.16). Show that ΔABC≅ΔABD

View SolutionABCD is a quadrilateral in which and∠DAB =∠CBA(see Fig. 7.17). Prove that
(i) ΔABD≅ΔBAC
(ii) BD = AC
(iii) ∠ABD =∠BAC

View SolutionD is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionABC is a triangle in which AB=AC.DandE are points on the sides ABandAC respectively, such that AD=AE. Show that the points B<C<EandD are concyclie.
View SolutionABC is an isosceles triangle in which AB=AC.BE and CF are its two medians. Show that BE=CF.
View Solution