ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC
To locate a point in the interior of triangle ABC that is equidistant from all three vertices (A, B, and C), we need to find the circumcenter of the triangle. The circumcenter is the point where the perpendicular bisectors of the sides of the triangle intersect. Here’s a step-by-step solution:
1. Draw Triangle ABC: Start by sketching triangle ABC with vertices A, B, and C.
2. Find the Midpoints: Calculate the midpoints of at least two sides of the triangle.
- For side AB, the midpoint M1 can be found using the formula:
M1=(xA+xB2,yA+yB2)
- For side BC, the midpoint M2 can be found similarly:
M2=(xB+xC2,yB+yC2)
3. Draw Perpendicular Bisectors:
- From midpoint M1, draw a line that is perpendicular to side AB. This line is the perpendicular bisector of side AB.
- From midpoint M2, draw a line that is perpendicular to side BC. This line is the perpendicular bisector of side BC.
4. Find the Intersection Point:
- The point where the two perpendicular bisectors intersect is the circumcenter (let's call it O) of triangle ABC. This point O is equidistant from all three vertices A, B, and C.
5. Verify Equidistance:
- To confirm that point O is equidistant from A, B, and C, measure the distances OA, OB, and OC. They should all be equal.
Final Result:
The point O, where the perpendicular bisectors of sides AB and BC intersect, is the required point in the interior of triangle ABC that is equidistant from all vertices.
- For side AB, the midpoint M1 can be found using the formula:
M1=(xA+xB2,yA+yB2)
- For side BC, the midpoint M2 can be found similarly:
M2=(xB+xC2,yB+yC2)
- From midpoint M1, draw a line that is perpendicular to side AB. This line is the perpendicular bisector of side AB.
- From midpoint M2, draw a line that is perpendicular to side BC. This line is the perpendicular bisector of side BC.
- The point where the two perpendicular bisectors intersect is the circumcenter (let's call it O) of triangle ABC. This point O is equidistant from all three vertices A, B, and C.
- To confirm that point O is equidistant from A, B, and C, measure the distances OA, OB, and OC. They should all be equal.
The point O, where the perpendicular bisectors of sides AB and BC intersect, is the required point in the interior of triangle ABC that is equidistant from all vertices.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-1 )35videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-2 )10videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.4)6videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner20videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
What is the number of points in the plane of a triangle ABC which are at equal distance from the vertices of the triangle ?
A0B1C2D3 - Question 2 - Select One
The coordinates of the point which is equidistant from the three vertices of the △AOB as shown in the figure is
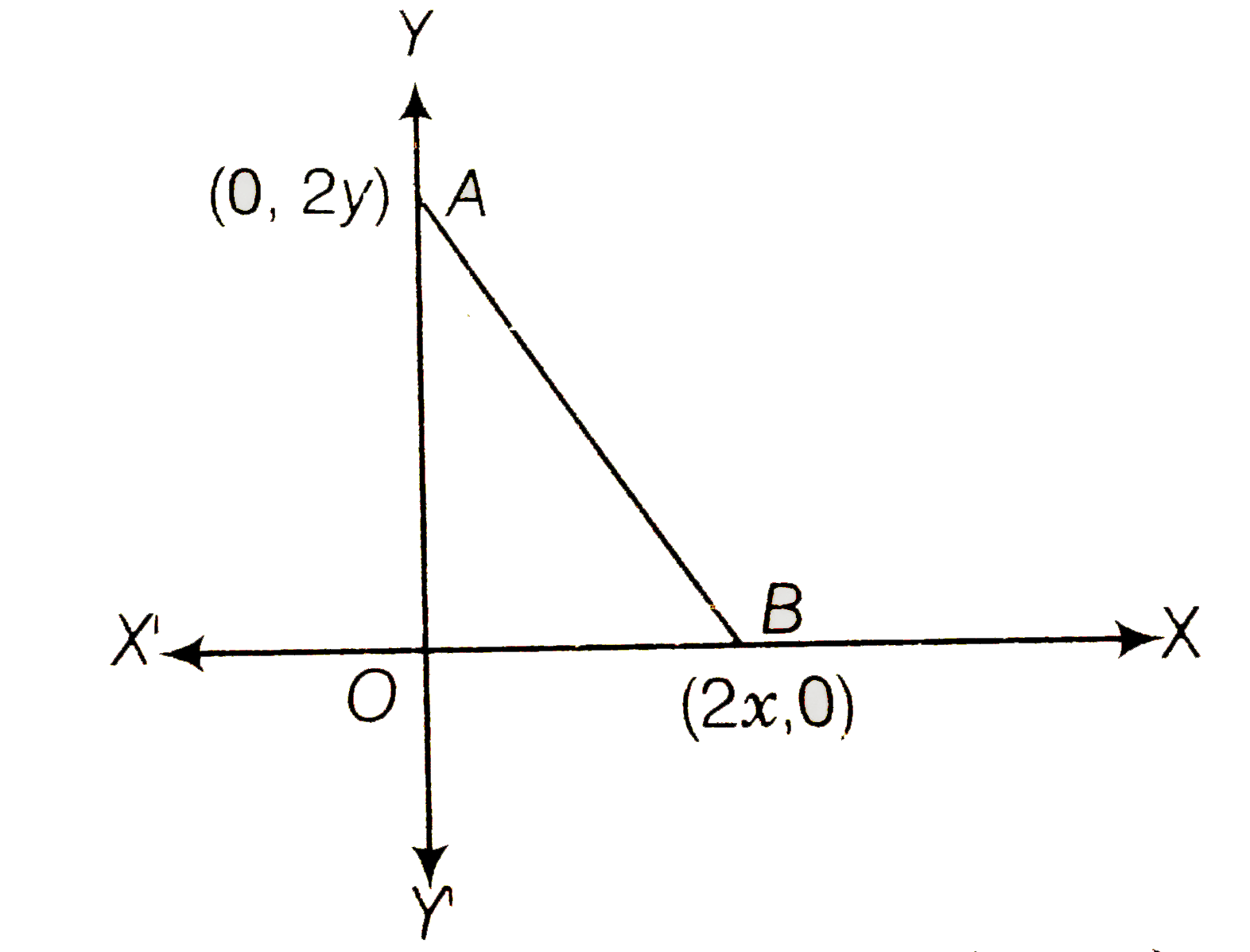 A(x,y)B(y,x)C(x2,y2)D(y2,x2)
A(x,y)B(y,x)C(x2,y2)D(y2,x2)
In a triangle, locate a point in its interior which is equidistant from all the sides of the triangle.
View SolutionFind the locus of the point which is equidistant from the sides AB and AC of triangle ABC.
View SolutionWhat is the number of points in the plane of a triangle ABC which are at equal distance from the vertices of the triangle ?
View SolutionProve that the mid-point of the hypotenuse of a right triangle is equidistant from its vertices
View SolutionIn a plane of triangle , the equidistant from three vertices of a triangle called its
View SolutionLet O be any point in the interior of ΔABC, prove that :
AB+BC+CA<2(OA+OB+OC)View Solution
